Problema
(Indicado a partir do 7º ano do E. F.)
Uma barra de chocolate PQRS de forma retangular e espessura constante será dividida em quatro pedaços por duas linhas retas, sendo que cada linha é paralela a dois lados opostos da barra, a partir de um ponto da diagonal PR como mostra a figura.
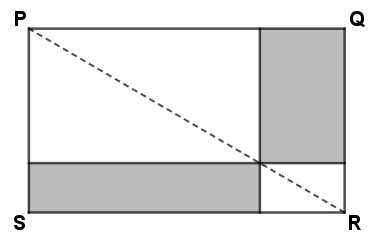
Depois de dividida a barra de chocolate, Eduardo e Diego escolheram, respectivamente, os pedaços A e B.
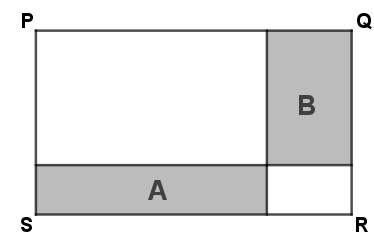
Qual dos dois pegou o pedaço maior e, portanto, com mais chocolate?
Justifique sua resposta.
Solução
Os retângulos A e B têm a mesma área.
Com efeito, observe que:
- a diagonal PR divide o retângulo PQRS em duas metades;
- a mesma diagonal divide os retângulos brancos ao meio.
Assim, a região em branco acima da diagonal e a região em branco abaixo da diagonal possuem a mesma área e, portanto, os retângulos A e B têm áreas iguais.
- – Não conseguiu concluir essa igualdade de áreas?
- A afirmação de que a diagonal PR divide o retângulo PQRS em duas metades nos garante que:
[tex]\qquad a_A+a_D+a_F=a_B+a_C+a_E.\qquad \textcolor{#800000}{(i)}[/tex] - Por outro lado, a afirmação de que a diagonal PR também divide os retângulos brancos ao meio nos garante que:
[tex]\qquad a_E=a_F~[/tex] e [tex]~ a_C=a_D.\qquad \textcolor{#800000}{(ii)}[/tex]
Então, acompanhe os cálculos a seguir.
- Sejam [tex]a_A[/tex], [tex]a_B[/tex], [tex]a_C[/tex], [tex]a_D[/tex], [tex]a_E[/tex] e [tex]a_F[/tex], respectivamente, as áreas das regiões A, B, C, D, E e F indicadas na figura abaixo.
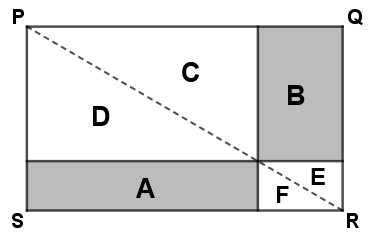
Agora, substituindo as igualdades [tex]\textcolor{#800000}{(ii)}[/tex] no lado esquerdo da igualdade [tex]\textcolor{#800000}{(i)}[/tex], segue que:
[tex]\qquad a_A+a_D+a_F=a_B+a_C+a_E\\
\qquad a_A+a_C+a_E=a_B+a_C+a_E\\
\qquad a_A+\cancel{a_C}+a_E=a_B+\cancel{a_C}+a_E\\
\qquad a_A+\bcancel{a_E}=a_B+\bcancel{a_E}\\
\qquad \textcolor{#800000}{\boxed{a_A=a_B}}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Um applet para ilustrar
Você pode utilizar o aplicativo disponibilizado abaixo para visualizar a solução do problema e, principalmente, observar que a igualdade das áreas dos retângulos A e B independe da posição do ponto da diagonal a partir do qual a barra de chocolate foi dividida.
Bom proveito!!!
