Problema
(Indicado a partir do 6º ano do E. F.)
Deve-se escrever um número natural em cada disco vazio da fila abaixo, de modo que a soma dos números em quaisquer três discos consecutivos seja sempre [tex]12[/tex].
Quais números podem ficar no último disco?
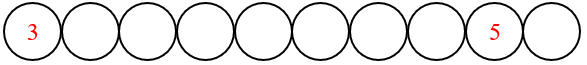
Solução
Tendo o primeiro disco numeração [tex]3[/tex] e sendo a soma das numerações de quaisquer três discos vizinhos igual a [tex]12[/tex], concluímos que a soma das numerações dos segundo e terceiro discos é [tex]9[/tex].
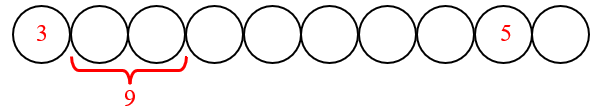
Dessa forma, o quarto disco tem o número [tex]3[/tex].
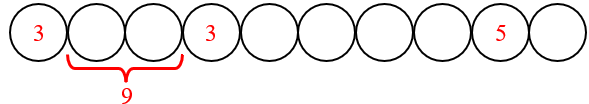
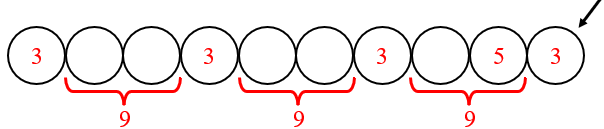
A partir daí obtemos um padrão que nos permite concluir que todo disco que ocupa posição [tex]3n + 1[/tex] ([tex]n[/tex] natural) terá numeração [tex]3[/tex], já que será antecedido por dois discos cuja soma das respectivas numerações é [tex]9[/tex].
Agora, perceba que o último disco está décima posição e [tex]10 = 3 \times 3 + 1[/tex], logo sua numeração é [tex] \,\fcolorbox{black}{#eee0e5}{$3$}\,[/tex].
Solução elaborada pelos Moderadores do Blog.
Participaram da discussão os Clubes: AS PRIMAS E EU; Mirim Aprendiz.