.Probleminha: Construindo Origami

Problema
(Indicado a partir do 9º ano do E. F.)

---

“O origami é a arte de dobrar papel. O termo deriva do japonês e junta as palavras “ori”, que significa “dobrar”, e “kami”, que é traduzido como “papel”. A técnica tradicional consiste em dobrar uma única folha de papel, quadrada, em uma escultura, sem fazer cortes ou colar o material. As principais formas encontradas nessa arte são animais, objetos, barcos e caixas.”

 
Naomi, em seu tempo vago, trabalha na construção dos mais diversos tipos de origamis. Certo dia, ela decidiu fazer um origami em que a primeira dobradura consiste da elevação do vértice [tex]D[/tex] da folha até o ponto médio [tex]M[/tex] do lado superior, como mostrado na figura abaixo.

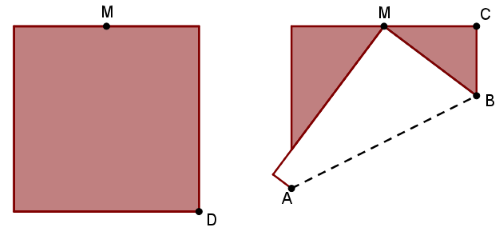
Sabendo que a área do triângulo [tex]BCM[/tex] é igual a [tex]6\;cm^2[/tex], determine a área da folha que Naomi estava utilizando.

Solução

---

A princípio, chamaremos de [tex]l[/tex] a medida do lado da folha, e de [tex]x[/tex] a medida do segmento [tex]\overline{BC}[/tex]. Sabendo que o segmento [tex]\overline{MC}[/tex] representa metade do lado da folha, ou seja, mede [tex]\dfrac{l}{2}[/tex], a base e a altura relativa do triângulo retângulo [tex]MCB[/tex] medem, respectivamente, [tex]\dfrac{l}{2}[/tex] e [tex]x[/tex], conforme figura abaixo.

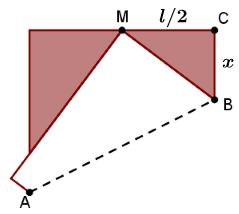
Sabendo que a área do triângulo é [tex]6\;cm^2[/tex], podemos obter

[tex]A = \dfrac{b \cdot h}{2} \Rightarrow 6 = \dfrac{\frac{l}{2} \cdot x}{2} \Rightarrow 6 = \dfrac{l \cdot x}{4} \therefore \boxed{lx = 24}.[/tex]

Agora, observe a hipotenusa de [tex]BCM[/tex]: como é uma dobra da folha inicial de lado [tex]l[/tex], quando juntamos a sua medida com o pedaço de [tex]l[/tex] equivalente a [tex]x[/tex], obtemos o lado [tex]l[/tex] novamente. Mais precisamente, podemos afirmar que [tex]x + BM = l[/tex], que é o equivalente a dizer que [tex]BM = l – x[/tex].

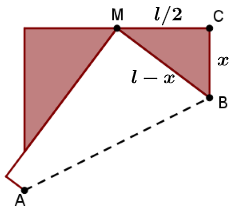
Aplicando o teorema de Pitágoras ao triângulo [tex]BCM,[/tex] obtemos:

[tex](l – x)^2 = x^2 + \left(\dfrac{l}{2}\right)^2 \Rightarrow l^2 – 2lx + x^2 = x^2 + \dfrac{l^2}{4}.[/tex]

Como já sabemos que [tex]lx = 24[/tex], podemos substituí-lo na igualdade acima e também cancelar [tex]x^2[/tex], que aparece em ambos os lados. Assim, podemos prosseguir:

[tex]l^2 – 2 \cdot (24) + \cancel{x^2} = \cancel{x^2} + \dfrac{l^2}{4} \Rightarrow l^2 – 48 = \dfrac{l^2}{4} \Rightarrow 4(l^2 – 48) = l^2 \Rightarrow 4l^2 – 192 = l^2 \Rightarrow 3l^2 = 192 \therefore l^2 = \dfrac{192}{3} = 64.[/tex]

Como um quadrado de lado [tex]l[/tex] possui área igual a [tex]l^2[/tex], a área da folha que Naomi estava usando é igual a [tex]64\;cm^2.[/tex]

---

Solução elaborada pelo COM Potências de Euler, com contribuições dos moderadores do Blog.