Problema
(Indicado a partir do 8º ano do E. F.)
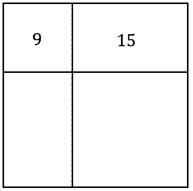
A figura abaixo representa um quadrado que foi repartido em [tex]4[/tex] regiões menores ([tex]2[/tex] quadrados e [tex]2[/tex] retângulos). As áreas do menor quadrado e de um dos retângulos estão indicadas na figura.
Qual a área do quadrado de maior região? E qual a área total da figura?
Solução
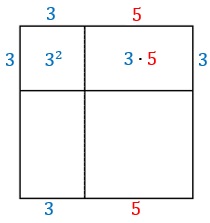
Pelo enunciado, como a área do quadrado menor vale [tex]9[/tex], então o lado do quadrado menor mede [tex]3[/tex].
Por outro lado, a área do retângulo vale [tex]15[/tex]. Como um de seus lados mede [tex]3[/tex] (lado do quadrado), o outro lado do retângulo mede [tex]5[/tex].
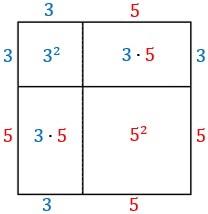
Por fim, como temos um quadrado de lado [tex]5[/tex], sua área será [tex]5^{2}=25[/tex] e o outro retângulo terá área [tex]3\cdot5=15[/tex].
Assim, a área do quadrado de maior região é [tex]\fcolorbox{black}{#eee0e5}{$25$}[/tex] e a área total da figura [tex]5^{2}+3\cdot5+3\cdot5+3^{2}=\fcolorbox{black}{#eee0e5}{$64$}[/tex], ambas medidas expressas na mesma unidade de área.
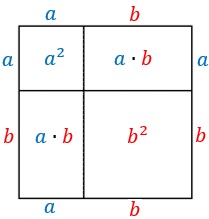
Note que esse probleminha nos mostra a interpretação geométrica de um dos mais famosos produtos notáveis:
- o Quadrado da Soma: [tex](a+b)^{2}=a^{2}+2\cdot a\cdot b+b^{2}.[/tex]
Solução elaborada pelos Moderadores do Blog.
