.Probleminha: Área do quadrado

Problema
(Indicado a partir do 9º ano do E. F.)

---

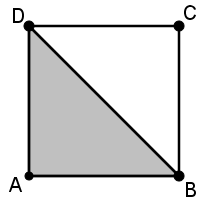
Determine a área do quadrado [tex]ABCD[/tex], sabendo que o perímetro do triângulo [tex]ABD[/tex] é igual a [tex]4~cm[/tex].

Solução

---

Sendo o lado do quadrado igual a [tex]l[/tex], temos [tex]BD = l\sqrt{2}[/tex]. Assim, o perímetro do triângulo [tex]ABD[/tex] é dado por [tex]2l+l\sqrt{2} = l(2+\sqrt{2})[/tex]. Por outro lado, sabemos que este valor deve ser igual a [tex]4~cm[/tex]. Portanto,

[tex]\qquad l(2+\sqrt{2})=4[/tex]
[tex]\qquad l=\dfrac{4}{2+\sqrt{2}}[/tex]
[tex]\qquad l=\dfrac{4(2-\sqrt{2})}{2}[/tex]
[tex]\qquad \boxed{l=2(2-\sqrt{2})}.[/tex]

Logo, a área do quadrado [tex]ABCD[/tex], é [tex]l^2 = [2(2-\sqrt{2})]^2 = (4-2\sqrt{2})^2 = 16-16\sqrt{2}+8 = \boxed{24-16\sqrt{2}~cm}[/tex].

---

Solução elaborada pelos Moderadores do Blog.