Problema
(Indicado a partir do 8º ano do E. F.)
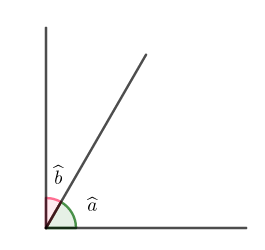
Considere os dois ângulos complementares mostrados na figura abaixo, cujas medidas indicaremos por [tex]\widehat{a}[/tex] e [tex]\widehat{b}[/tex].
Qual a medida do ângulo formado pelas bissetrizes desses dois ângulos?
Solução
Como os ângulos em questão são complementares, temos que a soma [tex]\widehat{a}+\widehat{b}[/tex] é igual a [tex]90^{\circ}[/tex]:
[tex]\qquad \widehat{a}+\widehat{b}=90^{\circ}.\qquad \qquad \textcolor{#800000}{(i)}[/tex]
Sabemos que a bissetriz divide um ângulo ao meio; assim, a bissetriz do ângulo que mede [tex]\widehat{a}[/tex] o dividirá em dois ângulos iguais, cada um medindo [tex]\dfrac{\widehat{a}}{2}[/tex].
Da mesma forma, a bissetriz do ângulo que mede [tex]\widehat{b}[/tex] o dividirá em dois ângulos, cada um medindo [tex]\dfrac{\widehat{b}}{2}~.[/tex]
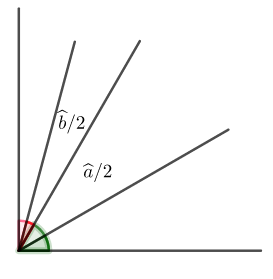
Assim, o ângulo formado entre as bissetrizes dos ângulos de medidas [tex]\widehat{a}[/tex] e [tex]\widehat{b}[/tex] mede:
[tex]\qquad \dfrac{\widehat{a}}{2}+\dfrac{\widehat{b}}{2}=\dfrac{\widehat{a}+\widehat{b}}{2}\stackrel{\textcolor{#800000}{(i)}}{=}\dfrac{90^{\circ}}{2}=\, \fcolorbox{black}{#eee0e5}{$45^{\circ}$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
