.Problemão: Volume complicado

Problema
(Indicado a partir da 2ª série do E. M.)

---

(FUVEST) No sólido da imagem a seguir, a base [tex]ABCD[/tex] é um retângulo de lados [tex]AB = 2\ell[/tex] e [tex]AD = \ell[/tex], as faces [tex]ABEF[/tex] e [tex]DCEF[/tex] são trapézios, as faces [tex]ADF[/tex] e [tex]BCE[/tex] são triângulos equiláteros e o segmento [tex]\overline{EF}[/tex] tem comprimento [tex]\ell[/tex].

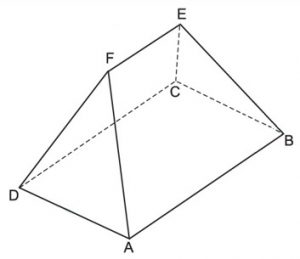
Encontre, em função de [tex]\ell[/tex], o volume desse sólido.

Solução

---

O sólido pode ser dividido em três novos sólidos:

1º) Um prisma triangular de altura [tex]\ell[/tex], cuja secção reta é um triângulo isósceles de lados congruentes com medida [tex]a[/tex] e altura [tex]h[/tex] (distância entre a aresta [tex]EF[/tex] e o plano do retângulo [tex]ABCD[/tex]).

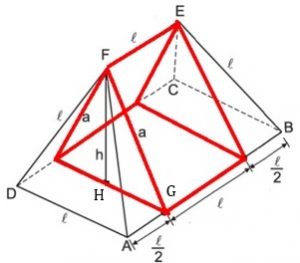
Pelo teorema de Pitágoras no triângulo [tex]FGA[/tex], temos que:

[tex]a^{2}+\left( \dfrac{\ell}{2} \right) ^2 = {\ell}^2 \Rightarrow a = \dfrac{\ell \sqrt{3}}{2}[/tex].

Novamente pelo teorema Pitágoras, agora no triângulo [tex]FHG[/tex]:

[tex]\left( \dfrac{\ell}{2} \right) ^2 + h^{2}=a^{2}\Rightarrow h=\dfrac{\ell \sqrt{2}}{2}[/tex].

Assim, pelo lembrete I, o volume desse prisma é:

[tex]V_{prisma}= \dfrac{\ell \cdot \dfrac{\ell \sqrt{2}}{2}}{2} \cdot \ell = \dfrac{{\ell}^3 \sqrt{2}}{4}[/tex].

2º) E duas pirâmides de base retangular e altura [tex]h[/tex] (distância entre a aresta [tex]EF[/tex] e o plano do retângulo [tex]ABCD[/tex]).

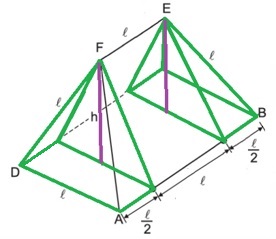
Pelo lembrete II, o volume de cada pirâmide é:

[tex]V_{pirâmide}= \dfrac {1}{3} \cdot \ell \cdot \dfrac{\ell}{2} \cdot \dfrac{\ell \sqrt{2}}{2} = \dfrac{{\ell}^3 \sqrt{2}}{12}[/tex].

Portanto, o volume do sólido é:

[tex]V_{sólido}= \dfrac{{\ell}^3 \sqrt{2}}{4} + 2 \cdot \dfrac{{\ell}^3 \sqrt{2}}{12} = \dfrac{5{\ell}^3 \sqrt{2}}{12}[/tex].

---

Solução elaborada pelos Moderadores do Blog.