Problema
(Indicado a partir do 9º ano do E. F.)
Um automóvel que sairá da cidade Pitágoras irá para a cidade Euler, em seguida irá para a cidade Gauss e, finalmente, retornará ao ponto inicial de partida fechando, assim, uma trajetória na forma de um triângulo equilátero.
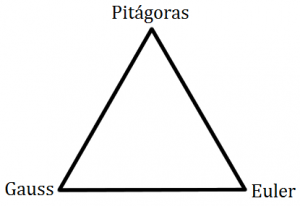
Sabendo que as velocidades de cada trecho são constantes e, respectivamente, iguais a [tex]v_1, v_2, v_3[/tex], qual a velocidade média ao longo de todo o percurso?
Solução
Seja [tex]d[/tex] a medida dos lados do triângulo, então os intervalos de tempo correspondentes ao percurso de cada lado são dados por
[tex]\qquad t_1=\dfrac{d}{v_1},\, t_2=\dfrac{d}{v_2},\, t_3=\dfrac{d}{v_3}[/tex].
Por outro lado, a soma dos intervalos de tempo é
[tex]\qquad t_1+ t_2+ t_3=\dfrac{d}{v_1}+\dfrac{d}{v_2}+\dfrac{d}{v_3}=d\left(\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}\right)[/tex].
Assim, como a velocidade média é calculada levando em conta o espaço percorrido e o tempo levado para percorrer tal espaço, então a velocidade média ao longo de todo o percurso apresentado é
[tex]\qquad v=\dfrac{3d}{t_1+t_2+t_3}=\dfrac{3d}{d\left(\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}\right) }=\dfrac{3}{\dfrac{1}{v_1}+\dfrac{1}{v_2}+\dfrac{1}{v_3}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
