Problema
(Indicado a partir do 1º ano do E. M.)
Nos últimos anos, o preço médio em reais por metro quadrado dos lotes de uma determinada região pode ser definido pela equação
[tex]\qquad \qquad \quad \quad \boxed{Preço (t) = – 2t^2+ 4t + 48} \, [/tex],
na qual [tex]t[/tex] representa o tempo, em anos, variando de [tex]t = – 3[/tex], no início de [tex]2011[/tex], a [tex]t=2[/tex], no início de [tex]2016 \, .[/tex]
Desta forma, responda:
a) Durante os anos de [tex]2011[/tex] a [tex]2016[/tex] houve uma crise no mercado imobiliário, em um ano em que o preço dos lotes por metro quadrado atingiu o valor máximo, decaindo no ano seguinte. Em que ano ocorreu a referida crise?
b) Uma pessoa comprou um lote de [tex]400 \, m^2[/tex] no início de [tex]2012[/tex], ao preço médio de mercado, e o vendeu, também ao preço médio de mercado, no início de [tex]2016[/tex]. A pessoa obteve lucro ou prejuízo na compra/venda? De qual valor?
Solução
a) A expressão [tex]\boxed{Preço (t) = – 2t^2+ 4t + 48} \, [/tex] que nos dá o preço médio por metro quadrado dos lotes define uma função quadrática cujo gráfico é uma parábola com concavidade voltada para baixo.
No nosso caso, a função está definida para [tex]t \in [-3 \, , \, 2][/tex] e seu gráfico é apresentado na figura abaixo.
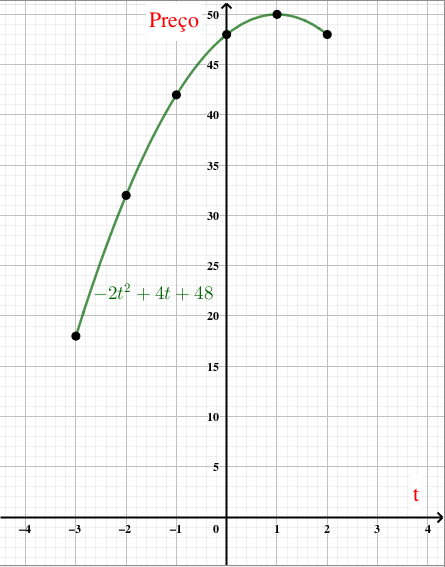
Conforme nos mostram os cálculos a seguir, o vértice da parábola é definido por um valor de [tex]t[/tex] que está no intervalo analisado e, como a parábola é côncava para baixo, o vértice é o ponto de máximo da função:
[tex]\qquad t_v=\dfrac{-b}{2a}=\dfrac{-4}{2\times(-2)}=1 \, [/tex].
Para finalizar o item (a), observe a tabelinha abaixo que mostra a correspondência entre os valores de [tex]t=-3,-2,-1,0,1,2,3 \, [/tex] e os anos de [tex]2011[/tex] a [tex]2015.[/tex]
[tex]\begin{array}{c|c|c|c|c}
-3 \leqslant t \lt -2&-2 \leqslant t \lt -1&-1 \leqslant t \lt 0&0 \leqslant t \lt 1&1 \leqslant t \lt 2\\
\hline
\text{ano de 2011}&\text{ano de 2012}&\text{ano de 2013}&\text{ano de 2014}&\text{ano de 2015}
\end{array}[/tex]
Assim, a crise aconteceu no início do ano [tex]2015[/tex] e se estendeu, pelo menos, até o final de [tex]2015[/tex].
b)
- Perceba na tabelinha acima que o início de [tex]2012[/tex] corresponde a [tex]t=-2 \, .[/tex] Assim, o valor do metro quadrado no início de ano é dado por:
[tex]\qquad Preço (-2) = – 2(-2)^2+ 4(-2) + 48 = – 8- 8+ 48=32 \, [/tex].
Logo, o preço do metro quadrado no início de [tex]2012[/tex] era de [tex]R\$\,32,00[/tex] e, portanto, o lote foi comprado a
[tex]\qquad 400\times R\$\,32,00=\boxed{R\$\,12.800,00} \, .[/tex] - O início de [tex]2016[/tex] corresponde a [tex]t=2[/tex] e o valor do metro quadrado é dado por:
[tex]\qquad Preço (2) = – 2(2)^2+ 4(2) + 48 = – 8+ 8+ 48=48 \, [/tex].
Dessa forma, o preço do metro quadrado no início de [tex]2016[/tex] era [tex]R\$48,00[/tex]. Logo, o lote foi vendido a
[tex]\qquad 400\times R\$\,48,00=\boxed{R\$\,19.200,00} \, .[/tex]
Com isso, concluímos que a pessoa em questão obteve um lucro de [tex] \, \fcolorbox{black}{#eee0e5}{$R\$\,19.200,00-R\$\,12.800,00=R\$\,6.400,00$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
