Problema
(Indicado a partir do 8º ano do E. F.)
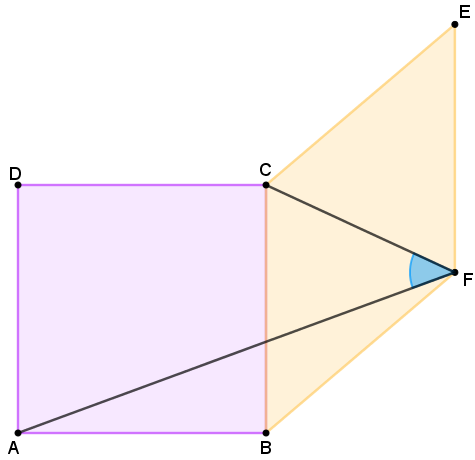
Considere um quadrado [tex]ABCD[/tex] e um losango [tex]BCEF[/tex] com o lado [tex]\overline{BC}[/tex] comum a ambos, como ilustra a figura abaixo.
Analise se existe algum losango em particular para o qual o ângulo indicado [tex]C\hat{F}A[/tex] é máximo.
Em caso afirmativo, indique qual é o losango e, caso contrário, justifique o porquê.
Solução
Seja [tex]\alpha[/tex] a medida em graus do ângulo [tex]C\hat{F}A[/tex].
Sejam, ainda, [tex]y\,[/tex] e [tex]\,z\,[/tex] as medidas em graus dos ângulos [tex]F\hat{B}C \,[/tex] e [tex]\, B\hat{C}F[/tex], respectivamente, conforme indica a figura abaixo.
Observe, inicialmente, que o triângulo [tex]ABF[/tex] é isósceles; logo, os ângulos [tex]B\hat{A}F\,[/tex] e [tex]\, A\hat{F}B[/tex] têm a mesma medida, digamos [tex]x[/tex] graus.
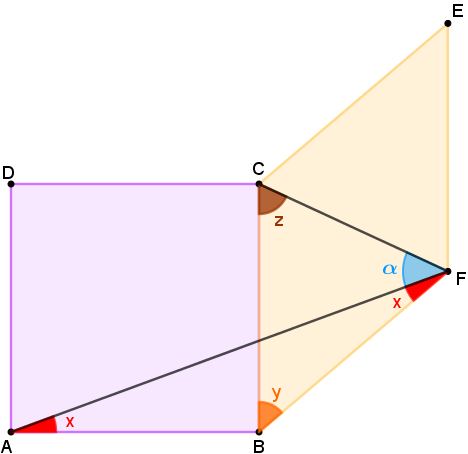
Como [tex]\overline{BC} \equiv \overline{BF}[/tex], o triângulo [tex]BCF[/tex] também é isósceles (de base [tex]\overline{CF}[/tex]) e, portanto, a medida do ângulo [tex]C\hat{F}B[/tex] é [tex]z[/tex]. Assim, [tex]\alpha + x = z[/tex].
Além disso, temos que
[tex]2z+y = 180^{\circ}.\quad\quad [/tex] (I)
Por outro lado, [tex]2x+y+90^{\circ} = 180^{\circ}[/tex], ou seja,
[tex]2x+y=90^{\circ}.\quad\quad [/tex] (II)
De (I) e (II), segue que:
[tex]\qquad \left(2z+y\right)-\left(2x+y\right)= 180^{\circ}-90^{\circ}\\
\qquad 2z-2x = 90^{\circ}\\
\qquad 2\left(z-x\right)= 90^{\circ}\\
\qquad z-x= 45^{\circ}.[/tex]
Assim, [tex]\alpha=z-x= 45^{\circ}[/tex], para qualquer losango, ou seja: não há um losango particular para o qual o ângulo indicado seja máximo.
Solução elaborada pelos Moderadores do Blog.
Visualização da solução
Para visualizar on-line a solução, utilize o applet abaixo.
Você também tem a opção de copiar o arquivo .ggb disponibilizado abaixo e utilizar o applet no GeoGebra do seu computador.
