Problema
(Indicado a partir do 3º ano do E. M.)
Seja [tex]P[/tex] um ponto pertencente à aresta [tex]\overline{AD}[/tex] do tetraedro regular [tex]ABCD[/tex], como representado abaixo.
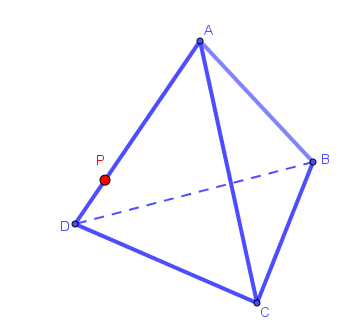
Se [tex]P[/tex] “desliza” sobre [tex]\overline{AD}[/tex], teremos o triângulo [tex]\triangle BPC[/tex] variando com [tex]P[/tex] e, consequentemente, o ângulo [tex]B\widehat{P}C[/tex] também variará.
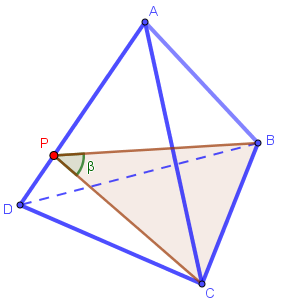
a) Verifique, justificando sua resposta, que o triângulo [tex]BPC[/tex] é sempre isósceles.
b) Determine a posição de [tex]P[/tex] para que a medida [tex]\beta[/tex] seja máxima. Justifique sua resposta.
Solução
a) Observe, inicialmente, que:
- [tex]\overline{CD}\equiv \overline{BD}[/tex] (são arestas do tetraedro)
- [tex]C\widehat{D}P \equiv B\widehat{D}P[/tex] (a medida dos ângulos é [tex]60^\circ[/tex])
- o lado [tex]\overline{DP}[/tex] é comum aos triângulos [tex]\triangle CDP[/tex] e [tex]\triangle BDP[/tex].
Logo, pelo critério de congruência LAL (lado, ângulo, lado), temos que [tex]\triangle CDP \equiv \triangle BDP[/tex] e, portanto, [tex]\overline{CP} \equiv \overline{BP}[/tex].
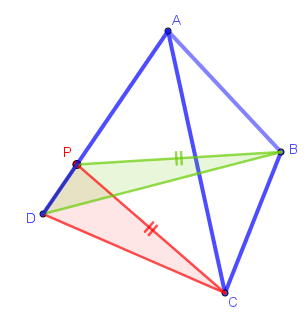
Assim, o triângulo [tex]\triangle BPC[/tex] é isósceles.
b) Observe que em um triângulo isósceles, se a base é fixa, quanto menor for a medida dos lados congruentes, maior será a medida do ângulo oposto à base. (Você pode visualizar essa propriedade no applet abaixo.)
Assim, no triângulo em questão, a menor medida possível para os lados do triângulo isósceles é quando estes coincidem com as alturas das faces às quais pertencem.
Portanto, a medida [tex]\beta[/tex] do ângulo [tex]B\widehat{P}C[/tex] será máxima quando [tex]P[/tex] for exatamente o ponto médio da aresta [tex]\overline{AD}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Visualização da propriedade
Para visualizar a propriedade, utilize o applet abaixo.
Você também tem a opção de copiar o arquivo .ggb disponibilizado abaixo e utilizar o applet no GeoGebra do seu computador.
