Problema
(Indicado a partir do 1º ano do E. M.)
A curva da figura é dada pela equação [tex]y=-x^2+4[/tex] e o triângulo [tex] ABC[/tex] é retângulo com ângulo reto no vértice [tex]C[/tex]. Calcule a área deste triângulo.
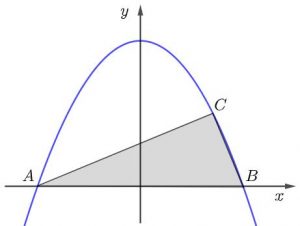

AJUDAS
(I) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(II) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(III) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução 1
Seja [tex]\overline{HC}[/tex] a altura do triângulo [tex]ABC[/tex] em relação ao vértice [tex]C[/tex]. A área de [tex]ABC[/tex] pode ser calculada por [tex]\dfrac{AB\cdot HC }{2}.[/tex]
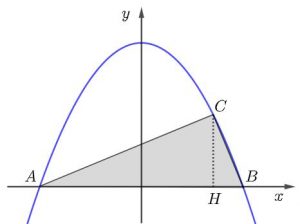
Os triângulos [tex]AHC[/tex] e [tex]CHB[/tex] são semelhantes por terem ângulos correspondentes iguais (caso A.A.). Assim,
[tex]\qquad \dfrac{HC}{AH}=\dfrac{HB}{HC}, [/tex]
ou seja,
[tex]\qquad HC^2=AH\cdot HB. \ \ \ \ \ \ \ \ \ \ \textcolor{#800000}{(1)}[/tex]
Como a equação da parábola pode ser escrita como [tex]y=-(x-2)(x+2)[/tex], então segue que
[tex]\qquad y=0 \ \ \Leftrightarrow \ \ (x-2)(x+2)=0 \ \ \Leftrightarrow \ \ x=2 \ \ \text{ou}\ \ x=-2.[/tex]
Com isso podemos concluir que [tex]A=(-2,0)[/tex], [tex]B=(2,0)[/tex] e [tex]AB=4[/tex] .
Sejam [tex](x_0,y_0) [/tex] as coordenadas do ponto [tex]C[/tex]. Observe que [tex]y_0=-(x_0-2)(x_0+2)[/tex] já que este ponto está sobre a parábola. Assim, [tex]HC=y_0[/tex], [tex]AH=x_0+2[/tex] e [tex]HB=2-x_0[/tex].
A igualdade [tex]\textcolor{#800000}{(1)}[/tex] pode ser então escrita como
[tex]\qquad y_0^2=(x_0+2)(2-x_0)=-(x_0+2)(x_0-2)=y_0.[/tex]
De acordo com a figura, [tex]y_0\gt 0[/tex], e podemos dividir os membros da última igualdade por [tex]y_0[/tex].
Assim,
[tex]\qquad y_0=1.[/tex]
Logo, [tex]HC=y_0=1[/tex] e a área do triângulo [tex]ABC[/tex] será [tex]\dfrac{4\cdot 1}{2}=2[/tex].
Solução elaborada pelos Moderadores do Blog.

AJUDA
Um triângulo é retângulo se, e somente se, pode ser inscrito em uma circunferência de diâmetro igual a um de seus lados.
Solução 2
Primeiramente, observe que a equação da circunferência no plano cartesiano é [tex]x^2+y^2=r^2[/tex], onde [tex]r[/tex] é o raio da circunferência. Este fato será necessário mais adiante!
As raízes da equação [tex]-x^2+4=0[/tex] são [tex]x_1=-2[/tex] e [tex]x_2=2[/tex], pois [tex]x^2=4[/tex] e por conseguinte [tex]x=\pm 2[/tex]. Daí, podemos concluir que o lado AB do triângulo ABC (que está sobre o eixo [tex]x[/tex]) mede [tex]4[/tex].
Como o triângulo ABC é retângulo em C, existe uma circunferência de diâmetro AB que contém o ponto C. Como [tex]AB=4[/tex], o raio da circunferência mede [tex]2[/tex]. Usando a equação da circunferência, temos que [tex]x^2+y^2=2^2=4[/tex]. Além disso, da lei da função, sabemos que [tex]y=-x^2+4[/tex], que é o mesmo que [tex]x^2+y=4[/tex]. Logo, basta resolvermos o sistema de equações:
[tex]\qquad \begin{cases}
x^2+y^2=4 \\
x^2+y=4
\end{cases}\implies y^2-y=0\implies y=0 \text{ ou } y=1.
[/tex]
Porém, para [tex]y=0[/tex] teríamos que a altura do triângulo [tex]ABC[/tex] em relação à base [tex]AB[/tex] é [tex]0[/tex], absurdo! Logo, [tex]y=1[/tex], e, portanto, a área de [tex]ABC[/tex] é dada por:
[tex]\qquad
Área_{ABC}=\dfrac{AB\cdot y}{2}=\dfrac{4\cdot 1}{2}=2.
[/tex]
Solução elaborada pelo Clube Phidias.
