Problema
(Indicado a partir do 9º ano do E. F.)
(Simulado SAS) Um fazendeiro, visando reduzir seu consumo de água, decidiu reestruturar seu sistema de irrigação por aspersão conectando, em um terreno plano, canos lineares com aspersores a uma linha principal fornecedora de água, conforme indicado na figura.
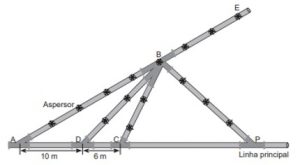
Para uma distribuição uniforme de água no terreno, foram inseridos os canos [tex]\overline{BD}[/tex] e [tex]\overline{BP}[/tex] ao sistema de irrigação antigo de tal forma que [tex]A\hat{B}D = C\hat{B}D[/tex] e [tex]C\hat{B}P = E\hat{B}P[/tex]. Sabendo que os pontos [tex]A[/tex], [tex]B[/tex] e [tex]E[/tex] estão alinhados, qual a distância, em metros, entre os pontos [tex]C[/tex] e [tex]P[/tex] no novo sistema de irrigação?

Lembretes e notações
(I) Teorema da bissetriz interna: A bissetriz de um ângulo interno de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.
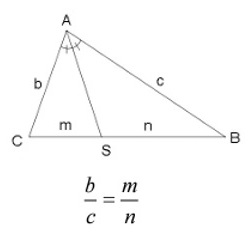
(II) Teorema da bissetriz externa: A intersecção da bissetriz externa com o prolongamento do lado oposto forma segmentos proporcionais aos lados adjacentes.
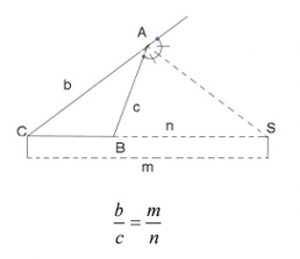
(III) Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex].
Solução
Do enunciado, percebe-se que [tex]\overline{BD}[/tex] e [tex]\overline{BP}[/tex] são bissetrizes interna e externa, respectivamente, do triângulo [tex]ABC[/tex], relativas ao ângulo [tex]A\hat{B}C[/tex].
Assim, pelo teorema das bissetrizes (interna e externa), tem-se [tex]\dfrac{AB}{BC}=\dfrac{10}{6}[/tex] e [tex]\dfrac{AB}{BC}=\dfrac{CP+16}{CP}[/tex].
Portanto, [tex]\dfrac{10}{6}=\dfrac{CP+16}{CP} \Rightarrow CP=24[/tex] m.
Solução elaborada pelos Moderadores do Blog.
