✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
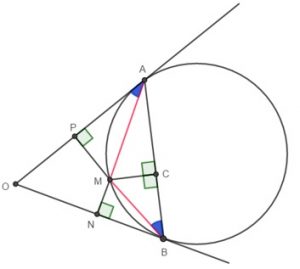
Na figura abaixo, temos duas semirretas com origem em [tex]O[/tex] tangentes a uma circunferência nos pontos [tex]A[/tex] e [tex]B[/tex].
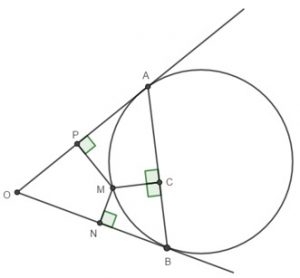
Calcule a medida do segmento [tex]\overline{MC}[/tex], sendo [tex]M[/tex] um ponto da circunferência, [tex]MN=2\text{ cm}[/tex] e [tex]MP=4,5\text{ cm}.[/tex]
Extraído de Geometria Plana, Professor Wilson Areias.

Lembretes e notações
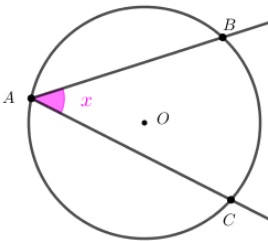
(1) Ângulo Inscrito: Dizemos que um ângulo é inscrito numa circunferência se este possui vértice sobre a circunferência e lados secantes a ela. Quando isso ocorre, a medida do ângulo é igual à metade da medida angular do seu arco correspondente (Arco definido pelo ângulo na circunferência e que não contém o seu vértice.).
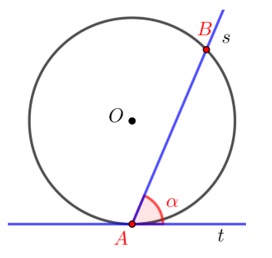
(2) Ângulo de segmento: Um ângulo é dito de segmento quando ele é definido por uma tangente a uma circunferência e uma secante que passa pelo ponto de tangência. Quando isso ocorre, a medida do ângulo é igual à metade da amplitude do arco delimitado pela corda.
(3) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline {AB}[/tex] e o seu comprimento por [tex]AB[/tex].
Solução
Inicialmente, vamos construir os segmentos [tex]\overline{MA}[/tex] e [tex]\overline{MB}[/tex], a partir da figura do enunciado.
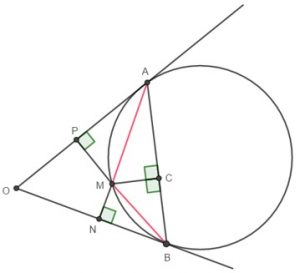
Note, pelo Lembrete 2, que o ângulo [tex]P\hat{A}M[/tex] é um ângulo de segmento e possui como medida metade da medida angular do arco [tex]\stackrel{\frown}{AM}[/tex].
Já [tex]A\hat{B}M[/tex], pelo Lembrete 1, é um ângulo inscrito e também possui como medida metade da medida angular do arco [tex]\stackrel{\frown}{AM}[/tex].
Logo, esses dois ângulos são congruentes.
Analogamente, o ângulo [tex]N\hat{B}M[/tex] é um ângulo de segmento e mede a metade da medida angular do arco [tex]\stackrel{\frown}{BM}[/tex] e [tex]B\hat{A}M[/tex] é um ângulo inscrito e também mede a metade da medida angular do arco [tex]\stackrel{\frown}{BM}[/tex].
Logo, esses dois ângulos também são congruentes.
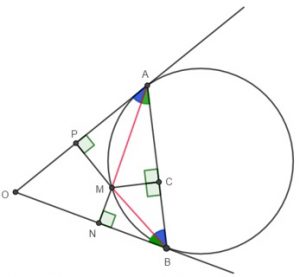
Portanto, os triângulos [tex]BCM[/tex] e [tex]APM[/tex] são semelhantes, assim como os triângulos [tex]ACM[/tex] e [tex]BNM[/tex].
- Da semelhança entre [tex]BCM[/tex] e [tex]APM[/tex], segue que:
[tex]\qquad \dfrac{MC}{PM}=\dfrac{MB}{MA}\\
\qquad \dfrac{MC}{4,5}=\dfrac{MB}{MA}\,. \qquad \textcolor{#800000}{(i)}[/tex] - Da semelhança entre [tex]ACM[/tex] e [tex]BNM[/tex], vem que:
[tex]\qquad \dfrac{MN}{MC}=\dfrac{MB}{MA}\\
\qquad \dfrac{2}{MC}=\dfrac{MB}{MA}\,. \qquad \textcolor{#800000}{(ii)}[/tex]
De [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], concluímos que:
[tex]\qquad \dfrac{MC}{4,5}=\dfrac{2}{MC}\\
\qquad {MC}^{2}=9 \,.[/tex]
Como [tex]MC[/tex] é a medida de um segmento (portanto um número positivo), temos [tex]\,\fcolorbox{black}{#eee0e5}{$MC=3\text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
