Problema
(Indicado a partir do 2º ano do E. M.)
A figura mostra um tetraedro [tex]ABCD[/tex] cujos vértices [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex] são vértices de um paralelepípedo retangular de dimensões com medidas [tex]x[/tex], [tex]y[/tex] e [tex]z[/tex].
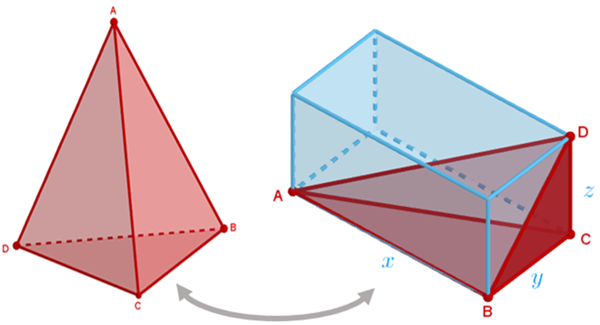
Se [tex]F_A[/tex], [tex]F_B[/tex], [tex]F_C[/tex] e [tex]F_D[/tex] são as áreas das faces do tetraedro opostas, respectivamente, aos vértices [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex], prove que [tex]\boxed{F^2_A + F^2_C= F^2_B + F^2_D}[/tex].
(Extraído de Maclaurin Olympiad, 2003-2009)
 |
Se vocês precisarem de uma ajuda para visualizar melhor o tetraedro e o paralelepípedo, cliquem no botão abaixo. |

AJUDA
► Definição:
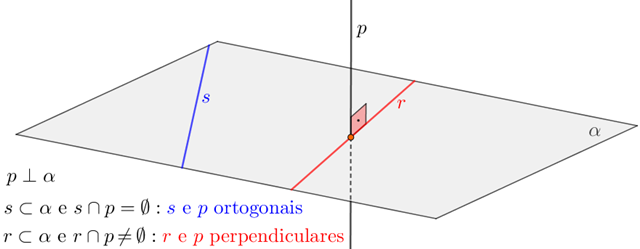
Uma reta e um plano são ditos perpendiculares se, e somente se, eles têm um ponto comum e a reta for perpendicular a todas as retas do plano que passam por esse ponto comum. Neste caso, dizemos também que a reta é perpendicular ao plano e que o plano é perpendicular à reta.
Na figura abaixo, a reta [tex]a[/tex] é perpendicular ao plano [tex]\alpha[/tex] ([tex]a \perp \alpha[/tex]) e o plano [tex]\alpha[/tex] é perpendicular à reta [tex]a[/tex] ([tex]\alpha \perp a[/tex]).
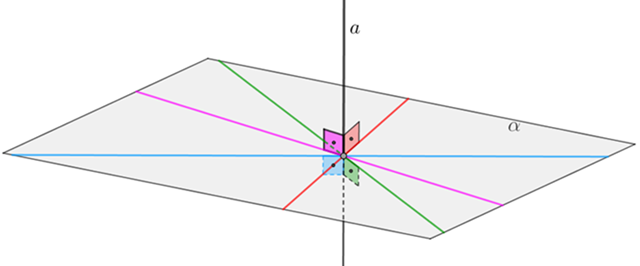
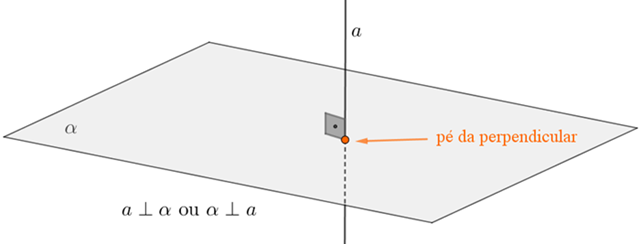
Se uma reta [tex]a[/tex] é perpendicular a um plano [tex]\alpha[/tex] (ou o plano [tex]\alpha[/tex] é perpendicular à reta [tex]a[/tex]), a intersecção de [tex]a[/tex] em [tex]\alpha[/tex] é chamada "pé da perpendicular".
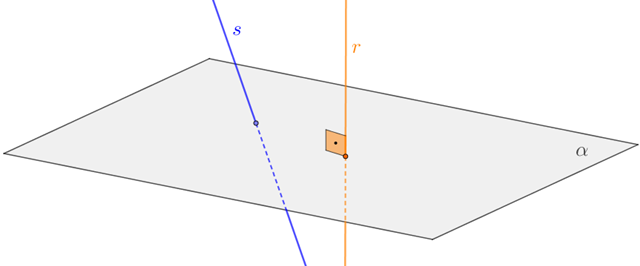
Uma reta e um plano que apresentem um único ponto em comum, mas não forem perpendiculares, são ditos oblíquos. Na figura a seguir, [tex]r[/tex] e [tex]\alpha[/tex] são perpendiculares, mas [tex]s[/tex] e [tex]\alpha[/tex] são oblíquos.
► Consequência da Definição:
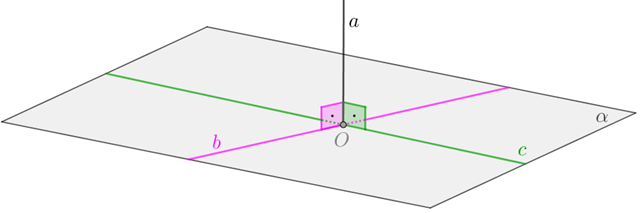
Se uma reta [tex]p[/tex] é perpendicular a um plano [tex]\alpha[/tex], então qualquer reta contida em [tex]\alpha[/tex] é dita ortogonal a [tex]p[/tex]. Particularmente, se as duas retas ortogonais intersectam-se, elas são ditas perpendiculares.
Assim, se [tex]p[/tex] é perpendicular a [tex]\alpha\;[/tex] e [tex]\;q[/tex] é uma reta contida em [tex]\alpha[/tex], então duas situações podem ocorrer::
– [tex]p[/tex] e [tex]q[/tex] intersectam-se no ponto em que [tex]p[/tex] "fura" o plano, e neste caso, [tex]p[/tex] e [tex]q[/tex] são perpendiculares;
– [tex]p[/tex] e [tex]q[/tex] não se intersectam ([tex]p \cap q=\emptyset[/tex]), e neste caso [tex]p[/tex] e [tex]q[/tex] são ortogonais.
► Teorema:
Se uma reta [tex]a[/tex] é perpendicular a duas retas [tex]b[/tex] e [tex]c[/tex] concorrentes de um plano [tex]\alpha[/tex], então [tex]a[/tex] é perpendicular ao plano [tex]\alpha[/tex].
Solução
Notações: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Na nossa solução, vamos considerar mais dois vértices do paralelepípedo: [tex]E\,[/tex] e [tex]\,F\,.[/tex]
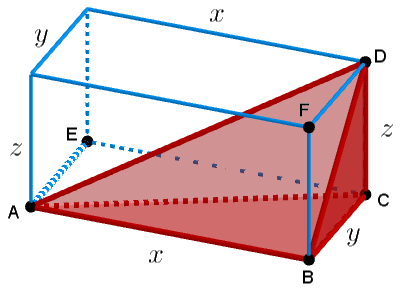
- Inicialmente, calculemos a área da face do tetraedro oposta ao vértice [tex]A[/tex]:
[tex]\qquad F_A=\dfrac{BC \cdot DC}{2}=\dfrac{y \cdot z}{2}[/tex]. - Agora, calculemos a área da face do tetraedro oposta ao vértice [tex]D[/tex]:
[tex]\qquad F_D=\dfrac{AB \cdot CB}{2}=\dfrac{x \cdot y}{2}[/tex]. - Para calcularmos [tex]F_B[/tex], precisamos notar que, como [tex]\overline{DC}[/tex] é perpendicular a [tex]\overline{BC}[/tex] e a [tex]\overline{EC}[/tex], então, pelo Teorema da Ajuda, [tex]\overline{DC}[/tex] é perpendicular ao plano que passa por [tex]ABCE[/tex]. Assim, [tex]\overline{DC}[/tex] é perpendicular a [tex]\overline{AC}[/tex] (Consequência da Definição). Com isso
[tex]\qquad F_B=\dfrac{AC \cdot DC}{2}[/tex].
Aplicando o Teorema de Pitágoras no triângulo [tex]ACB[/tex], obtemos: [tex]AC^2=x^2+y^2[/tex]. Logo,
[tex]\qquad F_B=\dfrac{\sqrt{x^2+y^2\,} \cdot z}{2}[/tex]. - De forma análoga, para calcularmos [tex]F_C[/tex], precisamos perceber que como [tex]\overline{AB}[/tex] é perpendicular a [tex]\overline{FB}[/tex] e a [tex]\overline{CB}[/tex], então, pelo Teorema da Ajuda, [tex]\overline{AB}[/tex] é perpendicular ao plano que passa por [tex]BCDF[/tex]. Assim, [tex]\overline{AB}[/tex] é perpendicular a [tex]\overline{BD}[/tex] (Consequência da Definição), e:
[tex]\qquad F_C=\dfrac{AB \cdot BD}{2}[/tex].
Aplicando, agora, o Teorema de Pitágoras no triângulo [tex]BDC[/tex], temos que [tex]BD^2=y^2+z^2[/tex] e, portanto:
[tex]\qquad F_C=\dfrac{x \cdot \sqrt{y^2+z^2}}{2}[/tex].
Agora, segue que:
[tex]\qquad F^2_A + F^2_C=\left(\dfrac{y \cdot z}{2}\right)^2+\left(\dfrac{x \cdot \sqrt{y^2+z^2}}{2}\right)^2\\
\qquad F^2_A + F^2_C=\dfrac{y^2 \cdot z^2+x^2 \cdot (y^2+z^2)}{4}\\
\qquad \boxed{F^2_A + F^2_C=\dfrac{y^2 \cdot z^2+x^2 \cdot y^2 + x^2 \cdot z^2}{4}}\,.[/tex]
Por outro lado,
[tex]\qquad F^2_B + F^2_D=\left(\dfrac{\sqrt{x^2+y^2} \cdot z}{2}\right)^2+\left(\dfrac{x \cdot y}{2}\right)^2\\
\qquad F^2_B + F^2_D=\dfrac{(x^2+y^2) \cdot z^2+x^2 \cdot y^2}{4}\\
\qquad F^2_B + F^2_D=\dfrac{x^2 \cdot z^2 +y^2 \cdot z^2+x^2 \cdot y^2}{4}\\
\qquad \boxed{F^2_B + F^2_D=\dfrac{y^2 \cdot z^2+x^2 \cdot y^2+x^2 \cdot z^2}{4}}\,.[/tex]
Logo, de fato, [tex]\, \fcolorbox{black}{#eee0e5}{$F^2_A + F^2_C= F^2_B + F^2_D$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
