Problema
(Indicado a partir do 3º ano do E. M.)
(UERJ-2010) A figura abaixo representa um recipiente cônico com uma solução aquosa de hipoclorito de sódio a [tex]27\%[/tex]. O nível desse líquido tem [tex]12[/tex] cm de altura.
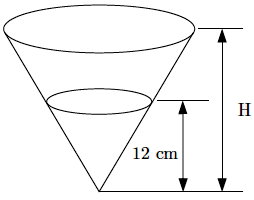
Para o preparo de um desinfetante, diluiu-se a solução inicial com água, até complementar o recipiente, obtendo-se a solução aquosa de hipoclorito de sódio a [tex]8\%[/tex].
Qual a altura [tex]H[/tex] desse recipiente em centímetros?

Ajuda
O volume do cone circular reto é um terço do produto entre a área da sua base e a medida da sua altura:
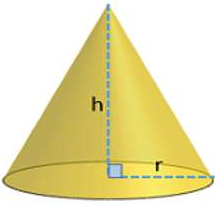
[tex]\qquad \qquad \dfrac{\text{área da base} \times \text{altura}}{3}. [/tex]
Se [tex]h[/tex] for o comprimento da altura e [tex]r[/tex] o do raio da base, então
[tex]\qquad \qquad Volume= \dfrac{\pi r^2h}{3}. [/tex]
Observação importante
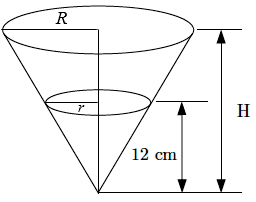
Neste problema, podemos estabelecer a relação entre os raios da base dos dois cones que aparecem na figura dada.
Suponhamos que esses raios meçam, em centímetros, [tex]r[/tex] e [tex]R[/tex], conforme mostra a figura ao lado.
Neste caso, pela semelhança entre os triângulos retângulos de bases com comprimentos [tex]r[/tex] e [tex]R[/tex] e respectivas alturas [tex]12[/tex] e [tex]H[/tex], obtemos:
[tex]\qquad \qquad \, \fcolorbox{black}{#d7d7d7}{$\dfrac{r}{R}=\dfrac{12}{H}$} \, .\qquad \textcolor{#800000}{(i)}[/tex]
Solução
Observe que a concentração inicial de hipoclorito de sódio na solução aquosa é de [tex]27\%[/tex] e queremos que essa concentração passe a ser de [tex]8\%[/tex].
Suponhamos, então, que [tex]V[/tex] seja o volume de hipoclorito presente na primeira solução aquosa e que, na diluição com água, o percentual de [tex]27\%[/tex] tenha sido em relação a um volume inicial total [tex]V_i[/tex] (água+hipoclorito).
Talvez uma regrinha de três ajude no entendimento desses volumes [tex]V[/tex] e [tex]V_i[/tex]:
[tex]\begin{array}{ccc}
V_i&\overline{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, } &100 \%\\
V& \overline{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, }&27\%\end{array}[/tex]
|
Assim, a concentração inicial de hipoclorito de sódio na solução aquosa pode ser expressa como: [tex]\qquad C=\dfrac{V}{V_i}=27\%[/tex] donde [tex]\qquad V=27\%\times V_i \, .\qquad \textcolor{#800000}{(ii)}[/tex] |
Uma concentração de [tex]27\%[/tex] de hipoclorito de sódio na solução aquosa significa que "para cada litro de solução temos [tex]270 \, ml [/tex] de hipoclorito". |
Com o acréscimo de mais água, o percentual em relação ao volume total final, [tex]V_f[/tex], foi de [tex]8\%[/tex]; porém, a quantidade de hipoclorito continua sendo [tex]V[/tex].
Ficamos, portanto, com a seguinte regra de três:
[tex]\begin{array}{ccc}
V_f&\overline{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, } &100 \%\\
V& \overline{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, }&8\%\end{array}[/tex]
|
A concentração final de hipoclorito de sódio na solução aquosa pode ser expressa como: [tex]\qquad C=\dfrac{V}{V_f}=8\%[/tex] donde [tex]\qquad V=8\%\times V_f \, .\qquad \textcolor{#800000}{(iii)}[/tex] |
A concentração de [tex]8\%[/tex] de hipoclorito de sódio na solução aquosa significa que "para cada litro de solução temos [tex]80 \, ml [/tex] de hipoclorito". |
Por [tex]\textcolor{#800000}{(ii)} \, [/tex] e [tex] \, \textcolor{#800000}{(iii)}[/tex] obtemos a relação entre [tex]V_i \, [/tex] e [tex] \, V_f[/tex]:
[tex] \, \, \\
\qquad 27\%\times V_i=V=8\%\times V_f\\
\qquad\dfrac{V_i}{V_f}=\dfrac{8}{27}\\
[/tex]
e essa relação, juntamente com a razão [tex]\textcolor{#800000}{(i)} \, [/tex], nos permitirá finalizar a solução do problema. Observe:
[tex] \, \, \\
\qquad \dfrac{V_i}{V_f}=\dfrac{8}{27}\\
\, \, \\
\qquad \dfrac{\frac{12 \pi r^2}{3}}{\frac{H \pi R^2}{3}}=\dfrac{8}{27}\\
\, \, \\
\qquad \dfrac{12 \pi r^2}{H \pi R^2}=\dfrac{8}{27}\\
\, \, \\
\qquad \dfrac{12 r^2}{H R^2}=\dfrac{8}{27}\\
\, \, \\
\qquad \dfrac{12}{H}\left(\dfrac{r}{R}\right)^2=\dfrac{8}{27}\\
\, \, \\
\qquad \dfrac{12}{H}\left(\dfrac{12}{H}\right)^2\stackrel{\textcolor{#800000}{(i)}}{=}\dfrac{8}{27}\\
\, \, \\
\qquad \left(\dfrac{12}{H}\right)^3=\dfrac{8}{27}\\
\, \, \\
\qquad H^3=\dfrac{12^3 \times 27}{8}\\
\, \, \\
\qquad H^3=5832\\
\, \, \\
\qquad H=18.[/tex]
Dessa forma, a altura [tex]H[/tex] do recipiente em questão é [tex] \, \fcolorbox{black}{#eee0e5}{$H=18 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
