Problema
(Indicado a partir do 2º ano do E. M.)
Em uma Olimpíada de Matemática, [tex]7501[/tex] estudantes fizeram uma prova de [tex]25[/tex] questões de múltipla escolha, com [tex]4[/tex] alternativas por questão, e todos os estudantes responderam a todas as questões.
Considere a afirmação:
- Pelo menos [tex]6[/tex] estudantes responderam de modo idêntico às [tex]k[/tex] primeiras questões da prova.
Qual é o maior valor de [tex]k[/tex] para o qual a afirmação é verdadeira?
Ajuda
 [tex]\textcolor{#800000}{(1)}[/tex] Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
[tex]\textcolor{#800000}{(1)}[/tex] Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas,
e todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra), então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex] (Se você não se lembra desse Princípio, clique AQUI.)
[tex]\textcolor{#800000}{(2)}[/tex] Princípio das casas de pombos:
Se tivermos [tex]n+1[/tex] pombos para serem colocados em [tex]n[/tex] casas, então pelo menos uma casa deverá conter mais de um pombo. (Se você não se lembra desse Princípio, clique AQUI.)
Solução
Como cada questão tem [tex]4[/tex] alternativas, pelo Princípio Multiplicativo, as [tex]k[/tex] primeiras questões podem ser respondidas de [tex]4\times 4 \times \cdots \times 4=4^k[/tex] modos.
[tex]\begin{array}{c c c c c}
\underline{\text{ 4 alternativas }}&\underline{\text{ 4 alternativas }}&\underline{\text{ 4 alternativas }}&\cdots &\underline{\text{ 4 alternativas }}\\
\text{Questão 1}&\text{Questão 2}&\text{Questão 3}&\cdots & \text{Questão k}
\end{array}[/tex]
Vamos agora analisar a ação de responder a todas as [tex]k[/tex] primeiras questões.
Já sabemos que essa ação pode ser feita de [tex]4^k[/tex] maneiras diferentes.
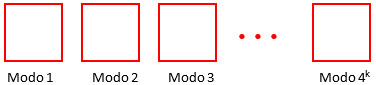
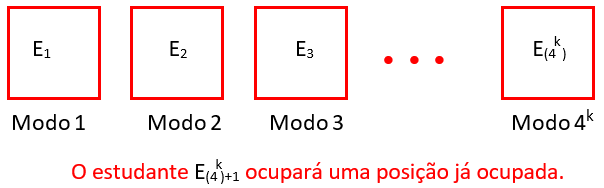
- Observe que se reunirmos [tex]4^k[/tex] estudantes, temos a possibilidade de que cada um responda as [tex]k[/tex] primeiras questões de uma maneira diferente dos demais, já que existem exatamente [tex]4^k[/tex] modos de responder a essas questões. Mas, se reunirmos [tex]4^k+1[/tex] estudantes, pelo menos dois desses estudantes irão responder da mesma forma, já que existem exatamente [tex]4^k[/tex] modos de se responder às [tex]k[/tex] questões.
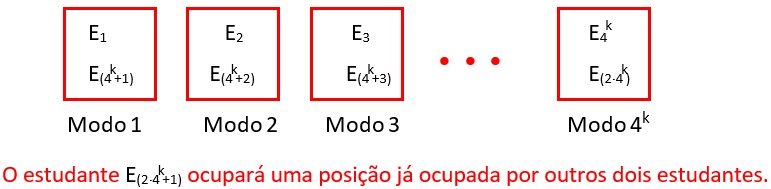
- Agora, se reunirmos [tex]2\cdot 4^k[/tex] estudantes, temos a possibilidade de que cada uma das [tex]k[/tex] primeiras questões seja respondida da mesma forma por dois estudantes, uma vez que temos [tex]4^k[/tex] modos de responder a essas questões. Mas, se reunirmos [tex]2 \cdot 4^k+1[/tex] estudantes, pelo menos três desses estudantes irão responder da mesma forma.
Se prosseguirmos com esse raciocínio, o "Princípio das casas de pombos" indica que deve-se ter pelo menos [tex]\boxed{5\cdot4^k+1}[/tex] estudantes para garantir que pelo menos seis estudantes respondam a estas [tex]k[/tex] primeiras questões do mesmo modo.
Dessa forma, segue que:
[tex]\qquad 5\cdot4^k+1\le7501[/tex]
[tex]\qquad 5\cdot4^k\le7500[/tex]
[tex]\qquad 4^k\le1500[/tex]
[tex]\qquad k\le 5.[/tex]
Portanto, o valor máximo para [tex]k[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\text{ cinco }$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
