Problema
Um artesão foi contratado para ornamentar os vitrais de uma igreja em fase final de construção. Para realizar o serviço, ele precisa de pedaços triangulares de vidro, os quais serão cortados a partir de um vidro pentagonal, com ou sem defeito, que possui [tex]n[/tex] bolhas de ar [tex](n = 0, 1, 2…)[/tex].
Sabendo que não há [tex]3[/tex] bolhas de ar alinhadas entre si, nem [tex]2[/tex] delas alinhadas com algum vértice do pentágono, e nem [tex]1[/tex] delas alinhada com dois vértices do pentágono, o artesão, para evitar bolhas de ar em seu projeto, cortou os pedaços de vidro triangulares com vértices coincidindo ou com uma bolha de ar, ou com um dos vértices do pentágono.
Nessas condições, determine a relação matemática entre o número máximo de triângulos [tex](T)[/tex] nos quais um vitral pode ser dividido pelo artesão em função do número [tex](n)[/tex] de bolhas de ar contidas no vidro utilizado.
Solução
Observe o pentágono abaixo.
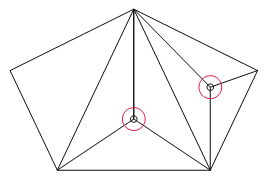
Seja [tex]T[/tex] o número de triângulos e [tex]n[/tex] o número de bolhas.
Observe que se não há três possíveis vértices (bolhas e vértices do pentágono) colineares, então é impossível que uma bolha esteja sobre uma aresta de um triângulo cortado.
- Isso significa que, para vitrais com defeito, se uma bolha não estiver no interior de um triângulo recortado, pois o artesão não deseja assim, ela será necessariamente vértice de um triângulo. Assim, cada bolha será vértice de pelo menos um triângulo.
Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], então [tex]T\cdot 180^\circ[/tex] deve ser igual à soma das medidas de todos os ângulos que possuem vértice nas bolhas ([tex]360^\circ\cdot n[/tex], pois temos [tex]360^\circ[/tex] ao redor de cada bolha) com as medidas de todos os ângulos cujo vértice esteja em um vértice do pentágono que somam [tex]540^\circ[/tex]. Logo, temos a seguinte relação:
[tex]T\cdot 180^\circ – 360^\circ n =540^\circ \qquad (:180^\circ)[/tex]
[tex]T-2n=3[/tex]
[tex]T=2n+3.[/tex]
Solução elaborada pelos Moderadores do Blog.
