.Problemão: Qual o valor máximo de M?

Problema
(Indicado a partir do 1º ano do E. M.)

Sendo $n$ um número real qualquer e $\boxed{ M = \dfrac {9}{ 2 \cdot \sqrt[3] { \dfrac { n^2}{12} + \dfrac { 82 – n }{3} } }}$ , determine o valor máximo que $M$ poderá assumir.

Lembretes

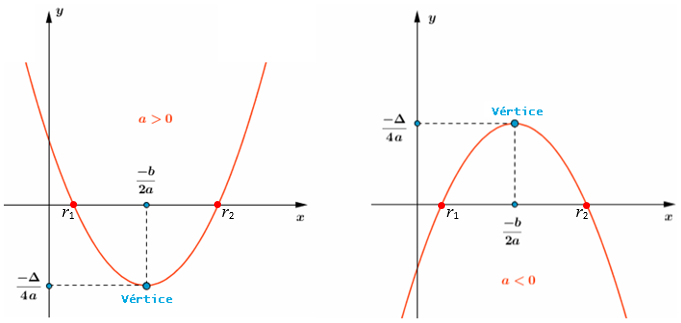
${\color{#800000}(1)}$ O gráfico de uma função quadrática $h:\mathbb{R}\rightarrow \mathbb{R}$ dada por $h(x)=ax^2+bx+c,\, a\not=0$ , é uma parábola com diretriz paralela ao eixo $Ox$ , eixo de simetria paralelo ao eixo $Oy$ , sendo sua concavidade voltada para cima se $a\gt 0$ e voltada para baixo se $a\lt0$ .

${\color{#800000}(2)}$ Se $\Delta= b^2-4ac$ , as coordenadas do vértice da parábola do gráfico de $h$ são dadas por:
$\qquad \qquad (x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)$ ,
sendo que $x_v=\dfrac{-b}{2a}\,$ e $\, y_v=\dfrac{-\Delta}{4a}$ indicam, respectivamente:

o ponto de mínimo e o valor mínimo da função $h$ , se a concavidade estiver voltada para cima;
o ponto de máximo e o valor máximo da função $h$ , se a concavidade estiver voltada para baixo.

Particularmente, se $\Delta \gt 0$ , $x_v$ é a média entre as duas raízes de $h$ : $x_v=\dfrac{r_1+r_2}{2}$

Visualizem as informações fornecidas no lembrete ${\color{#800000}(2)}$ , se $\Delta \gt 0$ ,
clicando no botão abaixo.

Solução

Sejam $n$ um número real e $M= \dfrac{9}{2 \cdot \sqrt[3] {\dfrac{ n^2}{12}+\dfrac{82-n}{3}}}.$
Para determinar o valor máximo que $M$ assume, vamos analisar inicialmente o seu denominador.
Para isso, seja $y =\dfrac{ n^2}{12}+ \dfrac {82-n}{3}$ e note que podemos reescrever $y$ na seguinte forma:

$\qquad y=\dfrac {n^2}{12}-\dfrac {4n}{12}+\dfrac {328}{12}= \boxed{\dfrac{n^2-4n+328}{12}}\, .$
Observe que o discriminante $\Delta$ da equação do segundo grau $n^2-4n+328=0\,$ é dado por $\, \Delta=(-4)^2-4\cdot 1\cdot 328=-1296$ . Como $\Delta \lt 0$ , a equação não possui raiz real e, sendo o coeficiente de $n^2$ positivo, conclui-se que $\, n^2-4n+328\gt0$ para todo $n\in\mathbb{R}.$
Dessa forma, temos que $\fcolorbox{#800000}{#ffffff}{$ \, y\gt 0 \text{ para todo } n\in\mathbb{R}\, $}\,$ , o que nos garante que $\fcolorbox{#800000}{#ffffff}{$ \text{o denominador de } M \, \acute{e} \text{ positivo para todo } n\in\mathbb{R}\, $}\, .$

Assim, para encontrarmos o valor máximo da fração $M$ , basta encontrarmos o valor mínimo de seu denominador, uma vez que o numerador permanece constante.

Note que este valor mínimo ocorre quando $y$ assume seu valor mínimo, dado pela ordenada $y_v$ do vértice da parábola que representa $y$ em função de $n$ .
Logo, pelo Lembrete, temos:
$\qquad y_v = \dfrac{-\bigg(\bigg(-\dfrac{4}{12}\bigg)^2-4\cdot \dfrac{1}{12}\cdot \dfrac{ 328}{12}\bigg)}{4\cdot \dfrac{1}{12}} =27$ .
Finalmente, o valor máximo de $M$ será dado por:
$\qquad M = \dfrac {9}{ 2 \cdot \sqrt[3]{27}}= \dfrac {9}{6}$ ,
isto é, $M = \fcolorbox{black}{#eee0e5}{$\dfrac {3}{2}$}\, .$

Solução elaborada pelos Moderadores do Blog.