Problema
(Indicado a partir do 6º ano do E. F.)
Emanuel e Natan foram a um acampamento juntos com seus professores. Nesse acampamento havia uma única barraca para todos os professores. Já os estudantes ficaram em [tex]10[/tex] barracas, cada uma delas com o mesmo número de pessoas.
Eles sabiam que o total de pessoas no acampamento era igual a [tex]41[/tex], e observaram que a quantidade de professores era igual à quantidade de estudantes de uma das barracas aumentada em [tex]8[/tex] (não se assuste, a barraca dos professores era bem grande!).
Quantos professores havia no acampamento?
Solução 1
Como a quantidade total de pessoas no acampamento, ou seja, a quantidade de professores somada com a quantidade de estudantes distribuídos em dez barracas, é igual a [tex]41[/tex] e a quantidade de professores é igual a de estudantes em uma de suas barracas aumentada em [tex]8[/tex], podemos escrever que a quantidade de pessoas em [tex]11 [/tex] barracas de estudantes aumentada em [tex]8[/tex] é igual a [tex]41[/tex].
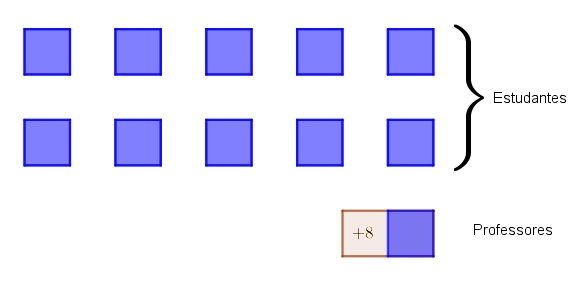
Logo, a quantidade de pessoas em [tex]11 [/tex] barracas de estudantes é igual a [tex]41-8 = 33 [/tex] e, portanto, a capacidade de uma barraca de estudantes é de [tex]3[/tex] pessoas.
Assim, a quantidade de professores no acampamento é [tex]\fcolorbox{black}{#eee0e5}{$3+8=11$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Consideraremos:
- número de professores: x;
- número de alunos: n;
- número de alunos, por barraca: y;
- total de pessoas no acampamento: 41;
assim, x+n =41.
Como as barracas foram distribuídas sendo uma para os professores e dez para os alunos, vem que:
[tex]\qquad \qquad [/tex] x+10y =41. [tex]\qquad[/tex](1)
A barraca dos professores tem oito pessoas a mais que uma barraca de alunos. Assim:
[tex]\qquad \qquad [/tex] x= y+8. [tex]\qquad[/tex] (2)
Substituindo (2) em (1), vem que:
[tex]\qquad \qquad [/tex] y+8 +10y =41
[tex]\qquad \qquad [/tex] 11y= 41-8
[tex]\qquad \qquad [/tex] 11y =33
[tex]\qquad \qquad [/tex] y=33/11
[tex]\qquad \qquad [/tex] y=3.
Logo, o número de alunos em cada barraca é 3 e o número de professores é x= y+3, ou seja, 11 professores.
Solução elaborada pelo COM OCTETO MATEMÁTICO, com contribuições dos Moderadores do Blog.
