Problema
(Indicado a partir do 2º ano do E. M.)
Observe o cubo desenhado na figura.
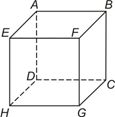
Considere todos os possíveis segmentos de retas determinados por cada dois vértices, entre os oito existentes.
Qual a probabilidade de se escolher um desses segmentos e ele passar pelo vértice [tex]G[/tex]?
Solução
- Há [tex]7[/tex] segmentos que contém [tex]G[/tex], todos eles com [tex]G[/tex] em uma de suas extremidades (nem todos aparecem desenhados na figura).
- Há um total de [tex]C_{8, 2}[/tex] segmentos possíveis.
Portanto, a probabilidade pedida é
[tex]\qquad \qquad P=\dfrac{n\acute{u}mero \, de \, casos\ favor\acute{a}veis}{n\acute{u}mero \, de \, casos\ possíveis}=\dfrac{7}{C_{8,2}}=\dfrac{1}{4}[/tex].
Solução elaborada pelos Moderadores do Blog .
