Problema
(Indicado a partir do 2º ano do E. M.)
Quebrando aleatoriamente um macarrão, de tamanho qualquer, em três partes, qual a probabilidade de que elas possam formar um triângulo?

Solução
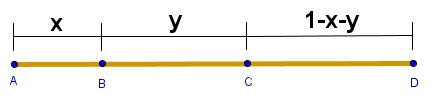
Considerando o nosso macarrão como unidade de comprimento temos que ele será dividido em [tex]3[/tex] partes, as quais identificaremos por [tex] \, x \, [/tex], [tex] \, y \, [/tex] e [tex] \, 1-x-y[/tex].
Notem que temos duas condições iniciais:
- as variáveis [tex]x[/tex] e [tex]y[/tex] representam valores positivos;
- a soma de [tex]x[/tex] e [tex]y[/tex] deve ser menor do que [tex]1[/tex] para garantir a existência do terceiro lado.
Pela desigualdade triangular (DT), temos que a soma de quaisquer dois lados deve ser maior ou igual do que o terceiro lado para que tenhamos, de fato, um triângulo (no caso em que é igual, temos um segmento de reta, considerado como um triângulo degenerado).
Sendo assim, temos, pela condição inicial:
- [tex]x > 0, [/tex]
- [tex]y>0 [/tex]
- [tex]x+y<1[/tex], ou seja, [tex] y<-x+1[/tex].
Isso significa que o par ordenado [tex](x,y)[/tex] que contém as variáveis iniciais de nosso problema pertence à região verde indicada na figura abaixo. Essa área representará, portanto, nosso espaço amostral.
Olhemos, agora, para as condições de interesse. Pela DT, temos que:
- [tex]x+ (1-x-y) ≥ y \implies y≤0.5, [/tex]
- [tex]y+ (1-x-y) ≥ x \implies x≤0.5, [/tex]
- [tex]x+y≥1-x-y \implies y≥-x+0.5[/tex].
Isso significa que o par ordenado [tex](x,y)[/tex] que contém as variáveis satisfazendo nossas condições de interesse pertence à região azul indicada abaixo.
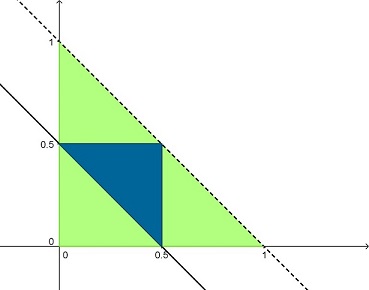
Temos, então, os chamados “casos possíveis” e “casos favoráveis” da nossa probabilidade, portanto:

Para finalizar, observem que a região azul corresponde a [tex] \, \dfrac{1}{4} \, [/tex] de nosso espaço amostral; assim, essa será a probabilidade procurada: [tex]\boxed{\frac{1}{4}_{\,}}[/tex].
Solução elaborada pelos Moderadores do Blog.
