Problema
(Indicado a partir do 2º ano do E. M.)
De quantas maneiras distintas podemos colorir a bandeira abaixo com as cores AZUL, BRANCA e VERMELHA, de modo que todas as cores apareçam com mesma área e que cada retângulo menor não seja pintado com mais de uma cor?
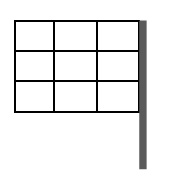
Considere que os nove retângulos menores têm mesma área.
Solução
▶ Para uma primeira cor, escolhemos três de nove retângulos para pintar, sendo que a ordem não importa. Assim, temos uma combinação de nove retângulos, tomados três a três ([tex]C_{9,3}[/tex]).
▶ Escolhidos os três primeiros retângulos, sobram seis para escolhermos três novos retângulos para pintarmos com a segunda cor; ou seja, uma combinação de seis retângulos tomados três a três ([tex]C_{6,3}[/tex]).
▶ Sobram apenas três retângulos para a última cor e, assim, não temos escolhas.
Pelo Princípio Multiplicativo (se um evento ocorre em sucessivas etapas, o total de possibilidades de ocorrência desse evento é determinado pelo produto das possibilidades de cada etapa), multiplicam-se esses resultados:
[tex]\qquad\qquad C_{9,3} \times C_{6,3} = 84 \times 20 = 1680[/tex].
Solução elaborada pelo Clube Fernandes Lima Alagoas.
Participou da discussão apenas o Clube Fernandes Lima Alagoas.
