Problema
(Indicado a partir do 3º ano do E. M.)
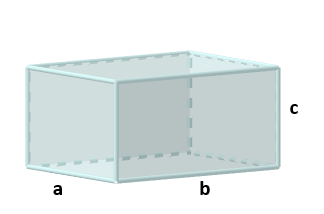
(Fundamentos de Matemática Elementar, Vol.10 – Adaptado) Considere o paralelepípedo retorretângulo de dimensões [tex]a, b[/tex] e [tex]c[/tex], ilustrado na figura.
Calcule os valores das dimensões [tex]a, b[/tex] e [tex]c[/tex] e do seu volume, sabendo que a soma de suas dimensões é [tex]45\;cm[/tex], que a sua diagonal da base mede [tex]25\;cm[/tex] e sua área total é igual a [tex]1300\;cm^2[/tex].
Solução
Devemos calcular os valores de [tex]a, b[/tex] e [tex]c[/tex] e também o volume do paralelepípedo retorretângulo, que é expresso por [tex] V=a\cdot b\cdot c.[/tex]
Consideremos que [tex]d=25\;cm[/tex] seja o comprimento da diagonal da base do paralelepípedo retorretângulo; então, do Teorema de Pitágoras, segue que:
[tex]\qquad d^2=a^2+b^2\\
\qquad a^2+b^2=25^2 \\
\qquad a^2+b^2=625. \;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(i)} [/tex]
Do enunciado, a soma das dimensões vale [tex]45\;cm[/tex], ou seja,
[tex]\qquad a+b+c=45.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(ii)}[/tex]
Elevando ao quadrado os dois membros da equação [tex]\textcolor{#800000}{(ii)}[/tex], obtemos que:
[tex]\qquad (a+b+c)^2=(45)^2\\
\qquad a^2+b^2+c^2+2(ab+ac+bc)=2025.\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(iii)}[/tex]
Sabemos que a área total do paralelepípedo retorretângulo, [tex]A_t[/tex], é igual a [tex]1300\;cm^2[/tex] e é expressa por
[tex]\qquad A_t=2(ab+ac+bc)\\
\qquad2(ab+ac+bc)=1300.\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(iv)}[/tex]
Substituindo [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(iv)}[/tex] em [tex]\textcolor{#800000}{(iii)}[/tex] segue que:
[tex] \qquad a^2+b^2+c^2+2(ab+ac+bc)=2025\\
\qquad 625+c^2+1300=2025\\
\qquad c^2=100 \\
\qquad c=10\;cm.[/tex]
Substituindo o valor de [tex]c=10[/tex] na equação [tex]\textcolor{#800000}{(ii)}[/tex], vem que
[tex] \qquad a+b=35\Rightarrow a=35-b.\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(v)}[/tex]
Substituindo [tex]\textcolor{#800000}{(v)}[/tex] em [tex]\textcolor{#800000}{(i)}[/tex] obtemos
[tex] \qquad (35-b)^2+b^2=625\Rightarrow 1225-70b+b^2+b^2=625\\
\qquad 2b^2-70b+600=0. \;\;\;\;\;\;\;\;\;\; \textcolor{#800000}{(vi)} [/tex]
Resolvendo a equação do segundo grau, [tex]\textcolor{#800000}{(vi)}[/tex], obtemos que [tex]b=20[/tex] ou [tex]b=15[/tex], donde [tex]a=15 [/tex] ou [tex]a=20.[/tex]
Assim, as dimensões do paralelepípedo retorretângulo são [tex] \, \fcolorbox{black}{#eee0e5}{$20\;cm $} \, [/tex], [tex] \, \fcolorbox{black}{#eee0e5}{$15\;cm $}[/tex] e [tex] \, \fcolorbox{black}{#eee0e5}{$10\;cm $}[/tex].
Como seu volume é [tex]V=a\cdot b \cdot c[/tex], então [tex]V=20\cdot 15\cdot 10= \, \fcolorbox{black}{#eee0e5}{$3000\;cm^3$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
