Problema
Por um ponto [tex]A[/tex] traçamos duas tangentes a uma circunferência dada. Os pontos de tangência são [tex]B[/tex] e [tex]C[/tex].
Pelo ponto [tex]D[/tex], situado no arco [tex]\stackrel{\frown}{BC}[/tex], traçamos uma tangente à circunferência a qual encontra os segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex] nos pontos [tex]E[/tex] e [tex]F[/tex], respectivamente.
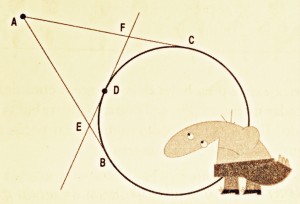
Sabendo que [tex]\overline{AB}[/tex] mede 8 cm, qual é o perímetro do triângulo [tex]AEF[/tex]?
Notações e Lembretes
✏ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
✏ Congruência de triângulos retângulos:
Se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então estes triângulos são congruentes.
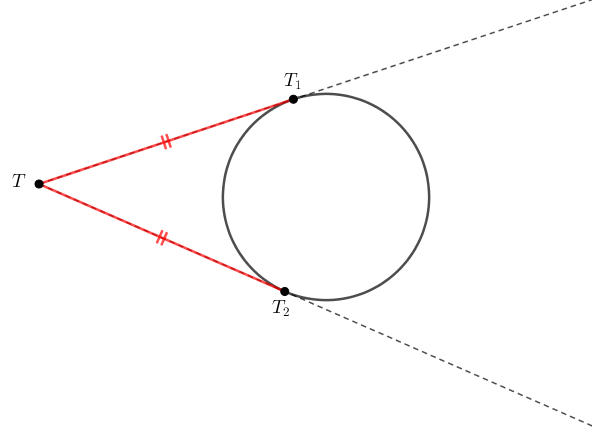
✏ Se de um ponto [tex]T[/tex] conduzirmos os segmentos [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] tangentes a uma circunferência, sendo [tex]T_1[/tex] e [tex]T_2[/tex] pontos da circunferência, então [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] têm o mesmo comprimento.
Solução
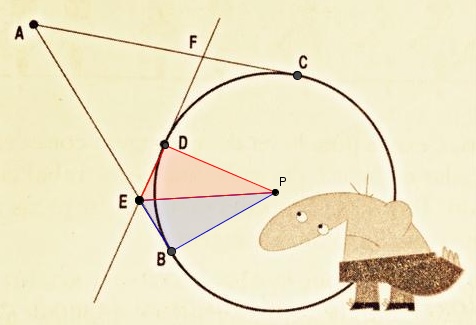
Seja [tex]P[/tex] o centro da circunferência dada.
Observe que o triângulo [tex]PBE [/tex] (em azul) e o triângulo [tex] PDE[/tex] (em vermelho), possuem:
(i) um lado em comum (segmento [tex]\overline{EP}[/tex]);
(ii) um ângulo reto (já que qualquer tangente a uma circunferência é sempre perpendicular ao raio no ponto de tangência);
(iii) dois outros lados com a mesma medida (os segmentos [tex]\overline{PB}[/tex] e [tex]\overline{PD}[/tex] são raios da circunferência).
- Dessa forma, os triângulos [tex]PBE~[/tex] e [tex]~PDE[/tex] são congruentes, pelo caso especial de congruência de triângulos retângulos.
- O mesmo raciocínio garante que os triângulos [tex]~PDF~[/tex] e [tex]~PCF~[/tex] também são congruentes.
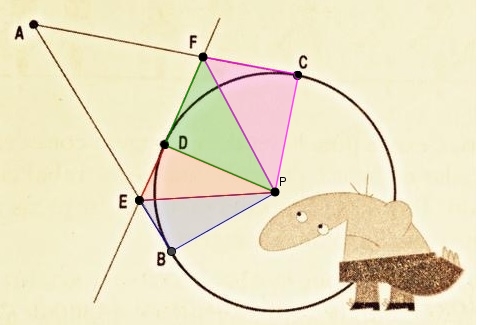
Assim, temos [tex]ED=EB~[/tex] e [tex]~DF=CF[/tex]; com isso, o perímetro do triângulo [tex]AEF[/tex], que denotaremos por [tex]Perim[/tex], corresponde à soma dos comprimentos dos segmentos [tex]\overline{AB}[/tex] e [tex]\overline{AC}[/tex], ou seja,
[tex]~~\\
\qquad Perim=AE+EF+FA\\
\qquad Perim=AE+(ED+DF)+FA\\
\qquad Perim=AE+(EB+CF)+FA\\
\qquad Perim=(AE+EB)+(CF+FA)\\
\qquad Perim=AB+CA\\
\qquad Perim=AB+AC\,.\\
[/tex]
Finalmente, um dos Lembretes nos garante que [tex]AC=AB[/tex]; logo, segue que:
[tex]~~\\
\qquad Perim=AB+AC\\
\qquad Perim=AB+AB\\
\qquad Perim=8+8\\
\qquad Perim=16\,.\\
[/tex]
Portanto, o perímetro do triângulo [tex]AEF[/tex] é igual a 16 cm.
Solução elaborada pelos Moderadores do Blog.
