Problema
(Indicado a partir do 8º ano do E. F.)
Em um país, certo dia, um avião partiu de cada cidade com destino à cidade mais próxima. Se as distâncias entre as cidades são duas a duas distintas, prove que em nenhuma cidade aterrissaram mais de cinco aviões.
Extraído de 144 Problemas de Matemática.

Fatos que ajudam
(I) Em todo triângulo, o maior ângulo se opõe ao maior lado.
(II) Em um triângulo escaleno, o maior ângulo é maior que [tex]60^\circ[/tex].
Solução
Suponha que chegaram pelo menos seis aviões em alguma cidade [tex]X[/tex], vindos das cidades [tex]C_1, C_2, \cdots, C_6[/tex]. Vamos obter um absurdo!
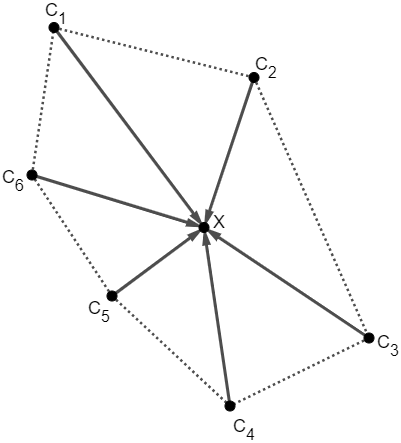
Considere o triângulo [tex]C_1C_2X[/tex]. Então, pela condição do enunciado, [tex]C_1X[/tex] e [tex]C_2X[/tex] são menores que [tex]C_1C_2[/tex], porque caso contrário o avião de [tex]C_1[/tex] teria partido para [tex]C_2[/tex] ou o de [tex]C_2[/tex] para [tex]C_1[/tex]. Assim, [tex]C_1\hat{X}C_2[/tex] é o maior ângulo deste triângulo e deve ser maior que [tex]60^\circ[/tex]. Como isso vale para qualquer um dos triângulos formados, temos
[tex]\qquad C_1\hat{X}C_2+C_2\hat{X}C_3+C_3\hat{X}C_4+C_4\hat{X}C_5+C_5\hat{X}C_6+C_6\hat{X}C_1\gt 6\times 60^\circ=360^\circ,[/tex]
que é um absurdo, pois a soma destes ângulos é igual a [tex]360^\circ[/tex].
Portanto, chegam no máximo cinco aviões em cada cidade.
Solução elaborada pelos Moderadores do Blog.
