Problema
(Indicado a partir do 2º ano do E. M.)
Num tabuleiro quadrado 4 x 4, deseja-se levar uma peça que está no quadrado superior esquerdo até o quadrado inferior direito.
A peça pode ser movimentada de um quadrado para um outro quadrado vizinho de três modos:
(1) descendo na vertical;
(2) descendo na diagonal à direita;
(3) afastando para o quadrado à direita.
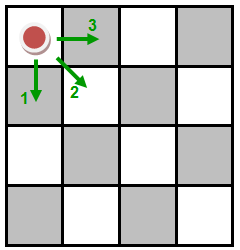 De quantos modos pode-se realizar o deslocamento da peça?
De quantos modos pode-se realizar o deslocamento da peça?
Solução
Os movimentos efetuados serão indicados por 1, 2 e 3.
Perceba que o destino final está três quadrados à direita e três quadrados abaixo do quadrado inicial; além disso, ao realizarmos o movimento em diagonal, estaremos afastando a peça, simultaneamente, para baixo e para a direita. Há, portanto, quatro tipos de percursos: com nenhum, um, dois ou três movimentos em diagonal.
Um percurso será indicado utilizando-se, repetida e respectivamente, os algarismos 1, 2 ou 3; assim, vejamos.
- Percursos sem o movimento 2 terão movimentos 1, 1, 1, 3, 3, 3 e cada permutação desses algarismos fornecerá um trajeto, não necessariamente diferente.
Há portanto [tex]{P_6}^{3 , 3} = \dfrac{6!}{3! \cdot 3!} = 20[/tex] percursos sem o movimento 2.
- Percursos com um movimento 2 terão movimentos 1, 1, 2, 3, 3 e cada permutação desses algarismos fornecerá um trajeto, não necessariamente diferente.
Há portanto [tex]{P_5}^{2 , 2, 1} = \dfrac{5!}{2! \cdot 2!} = 30[/tex] percursos com um movimento 2.
- Percursos com dois movimentos 2 terão movimentos 1, 2, 2, 3 e cada permutação desses algarismos fornecerá um trajeto, não necessariamente diferente.
Há portanto [tex]{P_4}^{2, 1, 1} = \dfrac{4!}{2!} = 12[/tex] percursos com dois movimentos 2.
- Percursos com três movimentos 2 terão movimentos 2, 2, 2 e cada permutação desses algarismos não modificará o trajeto.
Haverá, assim, um único percurso somente com movimentos 2.
Logo, há [tex]20 + 30 + 12 + 1 = 63[/tex] modos distintos de se fazer o deslocamento indicado.
Solução elaborada pelos Moderadores do Blog.
