Problema
(Indicado a partir do 1º ano do E. M.)
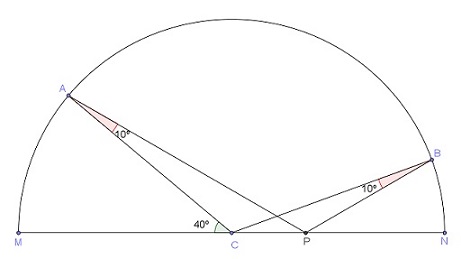
Sobre uma circunferência de diâmetro [tex]MN[/tex] e centro [tex]C[/tex] são tomados os pontos [tex]A[/tex] e [tex]B[/tex], distintos, de maneira que os ângulos [tex]C\hat{A}P[/tex] e [tex]C\hat{B}P[/tex] sejam iguais e meçam [tex]10^\circ[/tex], sendo [tex]P[/tex] um ponto do segmento [tex]CN[/tex], como ilustra a figura abaixo.
Se o arco [tex]AM[/tex] é de [tex]40^\circ[/tex], qual é a medida do arco [tex]NB[/tex]?
Solução
Seja [tex]r=CA=CB.[/tex]
Aplicando, inicialmente, o teorema do ângulo exterior no triângulo [tex]ACP[/tex], podemos afirmar que [tex]A\hat{C}M = C\hat{A}P+A\hat{P}C[/tex]; logo [tex] A\hat{P}C=30^{\circ}.[/tex]
Pela Lei dos Senos, aplicada aos triângulos [tex]ACP[/tex] e [tex]BCP[/tex], temos
[tex]\qquad \dfrac{sen10^{\circ}}{CP} = \dfrac{sen30^{\circ}}{r} \qquad [/tex] e [tex]\qquad \dfrac{sen10^{\circ}}{CP} = \dfrac{sen(B\hat{P}C)}{r}[/tex],
donde
[tex]\qquad sen30^{\circ}=sen(B\hat{P}C)[/tex].
Como [tex]A[/tex] e [tex]B[/tex] são pontos distintos, o ângulo [tex] B\hat{P}C[/tex] não pode ser um ângulo de [tex]30^{\circ}[/tex], logo [tex]B\hat{P}C+30^{\circ}=180^{\circ}[/tex] e, assim,
[tex]\qquad B\hat{P}C=180^{\circ}-30^{\circ}=150^{\circ}[/tex].
Deste modo, no triângulo [tex]BCP[/tex] temos que:
[tex]\qquad P\hat{C}B=180^{\circ}-150^{\circ}-10^{\circ}=20^{\circ},[/tex]
que é a medida do arco [tex]NB[/tex].
Solução elaborada pelos Moderadores do Blog.
