.Problemão: Medianas de um triângulo

Problema
(Indicado a partir do 9º ano do E. F.)

Ao traçarmos as três medianas de um triângulo qualquer, dividimos o mesmo em seis triângulos menores.
Mostre que esses seis triângulos são equivalentes, ou seja, possuem a mesma área.

Solução

Na resolução deste problema usaremos dois resultados bem conhecidos.

(1) As três medianas de um triângulo qualquer se intersectam num mesmo ponto. Este ponto é dito baricentro do triângulo.

O resultado (1) justifica a figura a seguir, na qual apresentamos um triângulo ABC, sendo D, E, F e G os pontos médios dos lados e o baricentro deste triângulo, respectivamente.

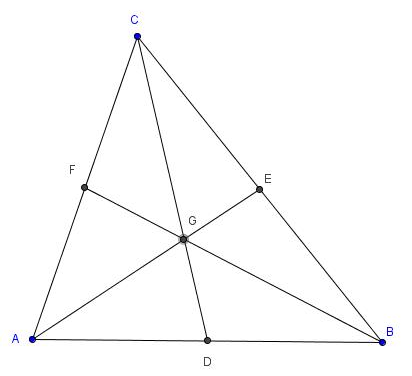
(2) Triângulos que tenham bases congruentes e mesma altura possuem mesma área.

Usando o resultado (2) no triângulo da nossa figura, perceba que:
   (i) os triângulos AGD e BGD possuem mesma área, que indicaremos por S; pois possuem bases AD e DB congruentes e a mesma altura relativa a essas bases (a distância de G à reta AB).
De modo análogo, observe que:
   (ii) os triângulos BGE e CGE possuem mesma área, que indicaremos por X;
   (iii) os triângulos CGF e AGF possuem mesma área, que indicaremos por Y;
   (iv) os triângulos CAD e CBD possuem mesma área; portanto, temos 2Y + S = 2X + S, de onde se conclui que Y = X;
   (v) os triângulos CAE e BAE possuem mesma área; portanto, temos 2Y + X = 2S + X, de onde se conclui que Y = S.
 

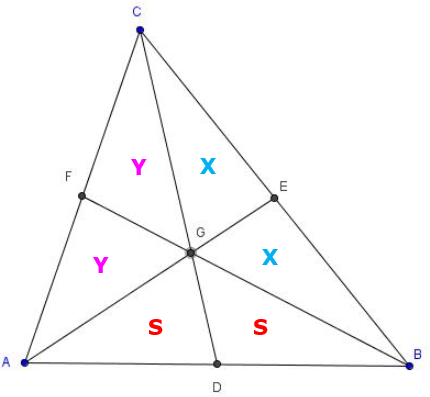
Temos, portanto, X = Y = S, o que nos leva a concluir que as medianas dividem o triângulo ABC em seis triângulos de mesma área S.

Solução elaborada pelos Moderadores do Blog.