Problema
(Indicado a partir do 7º ano do E. F.)
Um motorista viaja a uma velocidade constante e passa por um marco na estrada que contém um numeral de dois algarismos.
Após uma hora, o motorista passa por outro marco, cujo numeral contém os mesmos algarismos, mas na ordem inversa.
Uma hora depois, ele passa por um terceiro marco, cujo numeral contém os mesmos algarismos na ordem do marco inicial separados por um zero.
Qual a velocidade do motorista?

Lembrete
Quando um objeto está em movimento, ele muda de posição ao longo do percurso. A velocidade desse objeto é definida levando-se em consideração o espaço que ele percorreu em um determinado intervalo de tempo, ou seja, velocidade é a grandeza que mede quão rápido um objeto se desloca.
Se conhecermos a extensão do percurso e o tempo gasto pelo objeto para percorrê-la, podemos dividir o espaço percorrido pelo tempo total de percurso: a esse quociente chamamos velocidade média do objeto. Dessa forma, se [tex]\Delta s[/tex] for o espaço percorrido por um objeto no intervalo de tempo [tex]\Delta t[/tex], a velocidade média do objeto nesse movimento é dada pela expressão: [tex]\boxed{{\color{#800000}v_m=\dfrac {\Delta s}{\Delta t}}}[/tex]
Se a velocidade de um objeto é constante, ela é igual à velocidade média do objeto nesse movimento e, assim, temos:
[tex]\boxed{\text{velocidade}=\frac{\text{distância percorrida}}{\text{tempo gasto}}}[/tex].
É importante também nos atermos às unidades de medida. Se, por exemplo, a velocidade é em quilômetros/hora, a distância é em quilômetros e o tempo é em horas.
Solução
Sejam [tex]A[/tex] o algarismo das dezenas e [tex]B[/tex] o algarismo das unidades do primeiro marco.
Com os dados do problema, podemos imaginar as seguintes ilustrações dos três marcos:
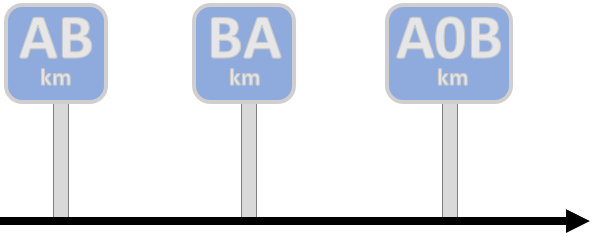
Essas ilustrações aparecem matematicamente representadas no esquema abaixo.
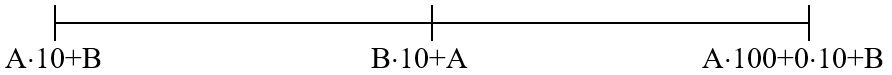
Como a velocidade é constante e os intervalos de tempo para se percorrer a distância entre dois marcos consecutivos são iguais (uma hora cada), concluímos que esses marcos estão igualmente espaçados, o que nos dá:
[tex]\qquad (10\cdot B+A)-(10\cdot A+B)=(100\cdot A+B)-(10\cdot B+A)[/tex]
[tex]\qquad B=6\cdot A \, .[/tex]
Mas, como [tex]B[/tex] é um algarismo, só podemos fazer [tex]A=1[/tex], donde vem que [tex]B=6[/tex].
Logo, os marcos são [tex]\boxed{16} \, , \, \boxed{61}[/tex] e [tex] \, \boxed{106} \, [/tex], e, consequentemente, a velocidade constante a que viaja o motorista pode ser assim calculada:
[tex]\qquad v=\dfrac{\text{distância percorrida}}{\text{tempo gasto}}=\dfrac{\text{(61 – 16) km}}{\text{1 hora}}= \, \fcolorbox{black}{#eee0e5}{$45\ km/h$} \, [/tex],
ou também
[tex]\qquad v=\dfrac{\text{distância percorrida}}{\text{tempo gasto}}=\dfrac{\text{(106 – 61) km}}{\text{1 hora}}= \, \fcolorbox{black}{#eee0e5}{$45\ km/h$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
