✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 3º ano do E. M.)
Considere todos os pares de números reais [tex]x[/tex] e [tex]y[/tex] que satisfazem a equação [tex]x^{2}+y^{2}=8x+6y-16[/tex].
Determine o valor máximo de [tex]x^{2}+y^{2}[/tex].
Lembretes e notações
✐ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
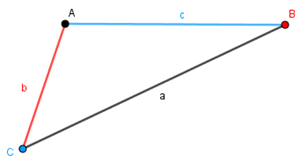(I) Desigualdade triangular: Em um triângulo, cada lado tem comprimento menor do que a soma dos comprimentos dos outros dois lados.
Assim, em um triângulo [tex]ABC[/tex] cujos lados [tex]\overline{AB}~[/tex], [tex]\overline{BC}~[/tex] e [tex]\overline{CA}~[/tex] medem [tex]c~[/tex], [tex]a~[/tex] e [tex]b~[/tex], respectivamente, então:
- [tex]\boxed{a \lt b+c}~[/tex], [tex]~\boxed{b \lt a+c}~[/tex] e [tex]~\boxed{c \lt a+b}.[/tex]
(II) A distância de um ponto [tex]P=(x, y)[/tex] à origem [tex]O=(0, 0)[/tex] em um plano cartesiano é dada por [tex]d=\sqrt{x^{2}+y^{2}}[/tex].
Solução
Inicialmente, vamos reescrever de outra maneira a igualdade [tex]x^{2}+y^{2}=8x+6y-16[/tex]; observe:
[tex]\qquad x^{2}+y^{2}=8x+6y-16\\
\qquad x^{2}-8x+y^{2}-6y=-16\\
\qquad x^{2}-8x\textcolor{#FF0000}{+4^{2}}+y^{2}-6y \textcolor{#FF0000}{+3^{2}}=-16 \textcolor{#FF0000}{+16+9}\\
\qquad(x-4)^{2}+(y-3)^{2}=3^{2}.[/tex]
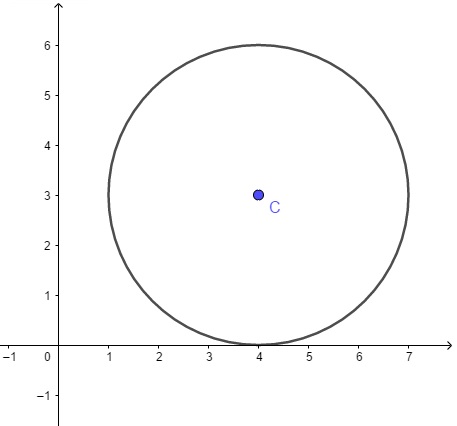
A última igualdade [tex](x-4)^{2}+(y-3)^{2}=3^{2}[/tex] representa em um plano cartesiano [tex]xOy[/tex] uma circunferência com centro [tex]C=(4, 3)[/tex] e raio [tex]r=3[/tex].
Agora, observe que, pelo Lembrete (II), a distância de um ponto [tex]P=(x, y)[/tex] à origem [tex]O=(0, 0)[/tex] no plano cartesiano é calculada por [tex]d=\sqrt{x^{2}+y^{2}}[/tex]. Logo, a expressão [tex]x^{2}+y^{2}[/tex] representa o quadrado da distância de um ponto [tex]P[/tex] à origem [tex]O[/tex]; perceba que esse " valor será máximo, quando a distância de [tex]P[/tex] à origem for máxima".
Assim, como queremos o valor máximo dessa distância, precisamos determinar o ponto da circunferência mais distante da origem:
- esse ponto é o ponto [tex]P[/tex] que está representado na imagem a seguir, e é um dos dois pontos da circunferência que estão alinhados com a origem do plano cartesiano e com o centro dessa circunferência.
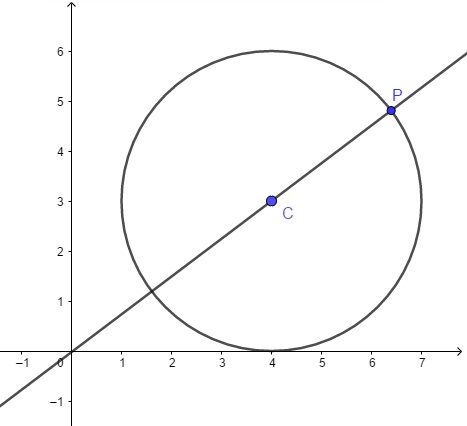
Vejamos a justificativa dessa afirmação.
- Tomemos um segundo ponto [tex]P'[/tex] na circunferência com centro [tex]C[/tex] e raio [tex]r=3[/tex], conforme vemos na próxima figura.
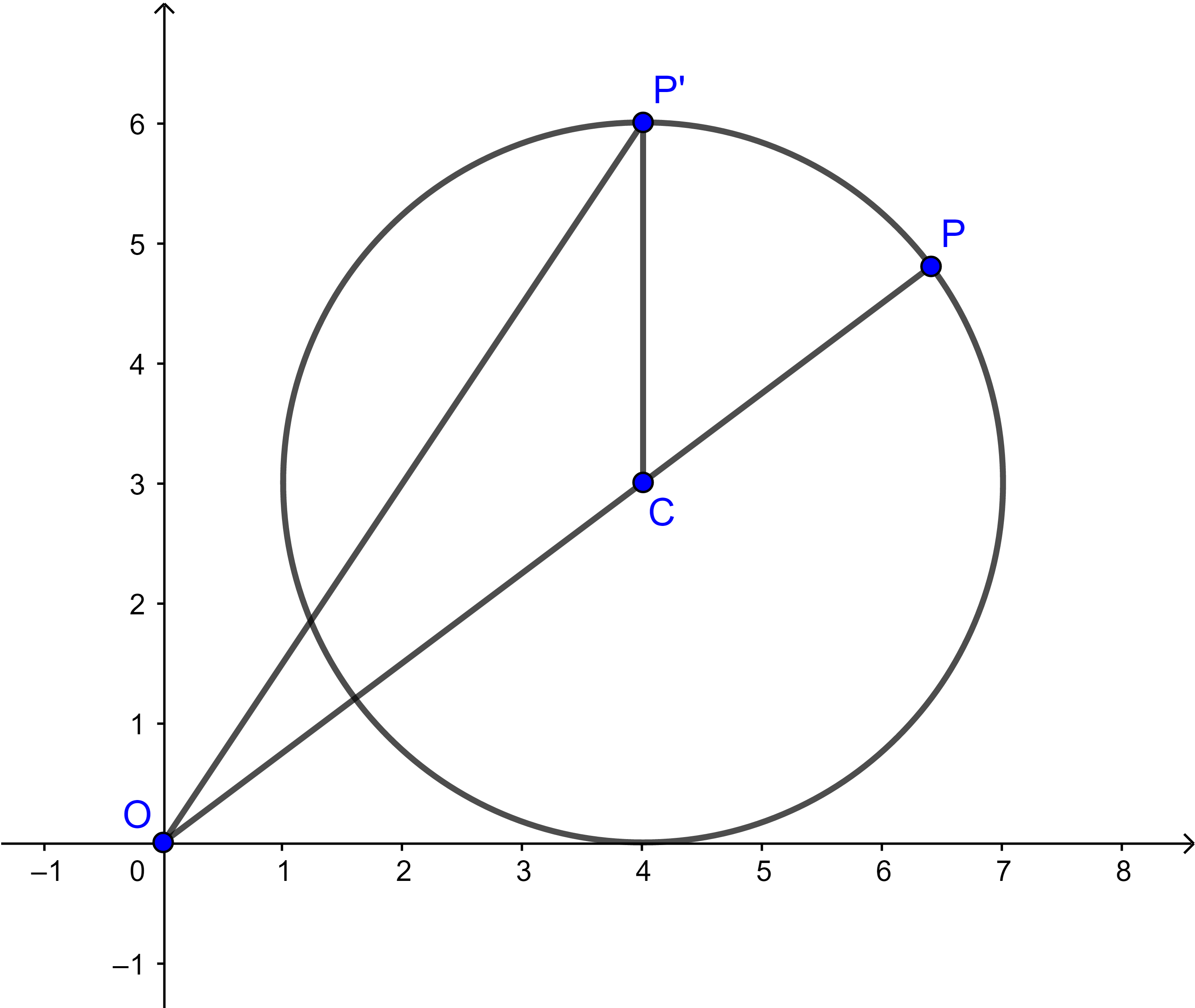
Observem que [tex]CP=CP'[/tex], pois [tex]\overline{CP}[/tex] e [tex]\overline{CP’}[/tex] são raios da circunferência, e [tex]OC+CP=OP[/tex] pois [tex]O[/tex], [tex]C[/tex] e [tex]P[/tex] estão alinhados. Logo, pela Desigualdade Triangular (Lembrete (I)),
[tex]\qquad OP’\lt OC+CP’=OC+CP=OP[/tex].
Portanto, para qualquer ponto [tex]P'[/tex] na circunferência, [tex]OP’\lt OP.[/tex]
Voltando ao problema, temos que:
- Pelo Teorema de Pitágoras, encontramos a distância da origem ao centro [tex]C[/tex].
- Já a distância de [tex]C[/tex] ao ponto [tex]P[/tex] é [tex]3[/tex] (raio da circunferência).
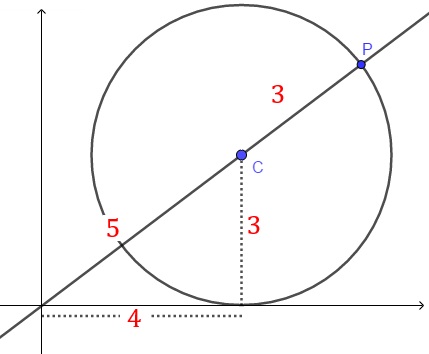
Com isso, a distância do ponto [tex]P[/tex] à origem é [tex]8[/tex] e, portanto, o valor máximo da expressão [tex]x^{2}+y^{2}[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$x^{2}+y^{2}=8^{2}=64$}[/tex] unidades de comprimento.
Você pode utilizar o aplicativo abaixo para visualizar a afirmação que fizemos de que "o ponto da circunferência que define a distância máxima à origem do plano cartesiano é um dos dois pontos que estão alinhados com a origem do plano cartesiano e com o centro dessa circunferência".
Um applet para ajudar
No applet abaixo, [tex]\textcolor{red}{P}[/tex] é um ponto da circunferência de centro em [tex]C\,[/tex] e raio [tex]\, 3[/tex].
Movimente o ponto [tex]\textcolor{red}{P}[/tex] e observe que, para cada posição de [tex]\textcolor{red}{P}[/tex], você visualizará a distância dele à origem do plano cartesiano [tex]xOy\,.[/tex]
Assim, você poderá visualizar em que posição [tex]\textcolor{red}{P}[/tex] define a maior distância da origem.
Instruções:
(1) Espere o applet carregar. (Ele pode demorar um pouquinho para carregar.)
(2) Para movimentar o ponto [tex]\textcolor{red}{P}[/tex], clique sobre ele, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto [tex]\color{red}{P}[/tex] e movimente-o.)
OBMEP_ srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
Solução elaborada pelos Moderadores do Blog.