Problema
(Indicado a partir do 8º ano do E. F.)
Para muitos, jogo de bilhar é pura diversão. Porém, para aqueles mais observadores é uma bela aula de geometria plana. Durante o jogo, cada vez que uma bola bate numa tabela, o ângulo de incidência é igual ao ângulo de reflexão. Assim quem conhece essa propriedade leva uma enorme vantagem no jogo.
Na mesa de bilhar representada na figura, existe uma bola em A, que deverá ser lançada na caçapa em D.
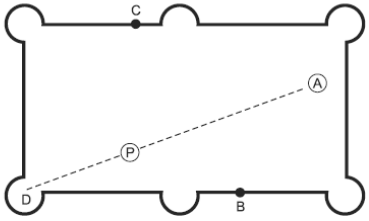
Porém, devido à obstrução gerada pela localização de outra bola em P, o jogador deverá usar todo o seu conhecimento de geometria plana e o seu talento para, com uma só tacada, encaçapar a bola que está em A na caçapa D. Para isso, ele usa os pontos B e C, indicados na figura, como referencial, para descrever a trajetória ABCD. Sabendo-se que BA é uma bissetriz externa e que DA é uma bissetriz interna do triângulo BCD, determine a medida do ângulo DÂB.
Solução
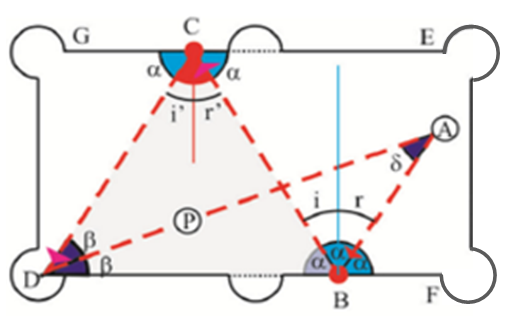
Como [tex]BA[/tex] é uma bissetriz externa do triângulo [tex]BCD[/tex], os ângulos [tex]F\hat{B}A[/tex] e [tex]C\hat{B}A[/tex] têm a mesma medida [tex]\alpha[/tex]; e como a medida do ângulo de incidência é igual à medida do ângulo de reflexão, então [tex]C\hat{B}D[/tex] mede [tex]\alpha[/tex]. Ou seja,
[tex]\qquad F\hat{B}A+C\hat{B}A+C\hat{B}D = 3\alpha = 180^{\circ}[/tex],
e, assim, [tex] \alpha = 60^{\circ}[/tex].
Percebam, agora, que os ângulos [tex]E\hat{C}B[/tex] e [tex]C\hat{B}D[/tex] são alternos internos e, deste modo, [tex]E\hat{C}B = \alpha = 60^{\circ}[/tex].
Os ângulos [tex]D\hat{C}G[/tex] e [tex]E\hat{C}B[/tex] têm a mesma medida (ângulo de incidência é igual ao ângulo de reflexão), então [tex]D\hat{C}G = 60^{\circ}[/tex].
Agora, como os ângulos [tex]D\hat{C}G[/tex] e [tex]C\hat{D}B[/tex] são alternos internos, concluímos que [tex]C\hat{D}B = 60^{\circ}[/tex]; e daí, como [tex]DA[/tex] é bissetriz interna, obtemos que [tex]B\hat{D}A = 30^{\circ}[/tex].
Já tínhamos que [tex]A\hat{B}D = 2\alpha = 120^{\circ}[/tex], logo,
[tex]\qquad D\hat{A}B = 180^{\circ}-(30^{\circ}+120^{\circ}) = 30^{\circ}[/tex].
Solução elaborada pelos Moderadores do Blog.
