Problema
Depois de acabada a aula de Biologia e já na aula de Matemática, na qual o professor estava trabalhando com Geometria, Rita e Ana estavam mais interessadas em desenhar do que em resolver problemas. Elas estavam desenhando girinos usando figuras geométricas.
Vejam abaixo os desenhos das “artistas”, com os respectivos nomes das autoras.
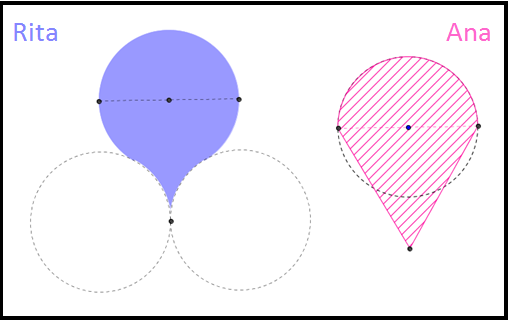
Os quatro círculos utilizados têm o mesmo raio e no desenho da Rita as três circunferências são duas a duas tangentes externamente. Também, no triângulo, que é equilátero, o lado na horizontal coincide com o diâmetro do círculo.
Comparadas as áreas das duas figuras apresentadas, podemos concluir que são iguais ou distintas? Se forem distintas, qual delas é maior? Justifique sua resposta.
Uma boa ideia
A figura abaixo nos dá uma ideia inicial:sobrepor os dois desenhos dos girinos.
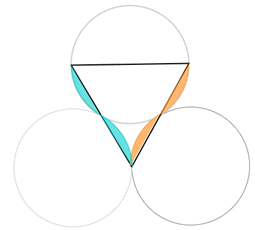
Ao fazermos a sobreposição, parece que as áreas são iguais, não é?
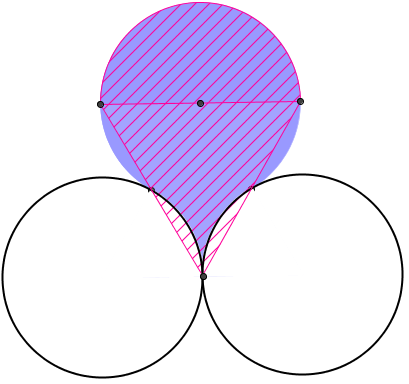Embora seja uma boa pista, apenas essa visualização não é uma solução para o problema.
Solução
Sejam [tex]A_c[/tex] e [tex]A_t[/tex] as áreas dos círculos e do triângulo, respectivamente, que aparecem nos desenhos.
- A área da figura que representa o girino desenhado por Ana é fácil de ser calculada, já que o desenho do girino rosa é formado pelo triângulo e por um semicírculo definido por um dos círculos utilizados:
[tex]\qquad \qquad G_{A}=\boxed{\dfrac{A_c}{2}+A_t}. \qquad \qquad (i)[/tex] - A área da figura que representa o girino desenhado por Rita é a área [tex]A_c[/tex] do circulo mais a área que corresponde à, digamos, cauda do girino. Vejam:
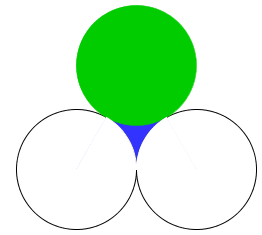Precisamos, então, calcular a área da figura correspondente à cauda e para isso a próxima figura pode nos ajudar.
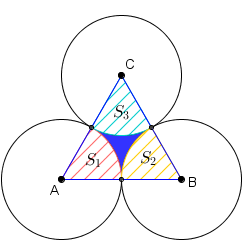
Observem que o triângulo [tex]ABC[/tex] com vértices nos centros dos três círculos desenhados por Rita é equilátero, assim ele define os três setores circulares [tex]S_1[/tex], [tex]S_2[/tex] e [tex]S_3[/tex], cada um com ângulo central de [tex]60^{\circ}[/tex]. Notem, também, que a área da cauda é a área [tex]A_t[/tex] menos as áreas desses três setores circulares.
Como [tex]60^{\circ}=\dfrac{360^{\circ}}{6}[/tex], a área de cada um desses setores corresponde à [tex]\dfrac{1}{6}[/tex] de [tex]A_c[/tex] e, assim, a área da figura correspondente à cauda será dada por
[tex]\qquad \qquad A_t-3 \cdot \dfrac{A_c}{6}=A_t-\dfrac{A_c}{2}[/tex].
Com isso a área da figura que representa o girino desenhado por Rita é :
[tex]\qquad \qquad G_{R}=A_c+\left(A_t-\dfrac{A_c}{2}\right)=\boxed{\dfrac{A_c}{2}+A_t}. \qquad \qquad (ii)[/tex]
Assim, por [tex](i)[/tex] e [tex](ii)[/tex], temos que, de fato, as áreas dos girinos desenhados por Ana e Rita são iguais.
Solução elaborada pelos Moderadores do Blog.