Problema
(Indicado a partir do 3º ano do E. M.)
(Unesp – Adaptado) Uma empresa oferece frete gratuito para entregas do seu produto em um raio de até [tex]30\ km[/tex] do depósito. Para a distância que ultrapassar [tex]30\ km[/tex], medida em linha reta desde o depósito, a empresa cobra [tex]R\$\, 10,00[/tex] por cada quilômetro que ultrapasse os [tex]30\ km[/tex] iniciais gratuitos. Essa cobrança também é feita de forma proporcional em caso de frações de quilômetros.
Um certo consumidor do produto reside [tex]25\ km[/tex] a oeste do depósito e [tex] y[/tex] [tex]km[/tex] ao sul.
(a) Determine o valor máximo de [tex]y[/tex] para que esse consumidor tenha direito ao frete gratuito na entrega do produto em sua residência.
(b) Determine o custo do frete [tex]C[/tex] (em reais) para esse consumidor, em função de [tex]y[/tex], para o caso em que [tex]C(y)\neq0[/tex].
Solução 1
A partir de um plano cartesiano, podemos interpretar a região em que o frete é gratuito como um círculo de raio [tex]30[/tex] centrado no depósito e considerar o depósito como o ponto de coordenadas [tex](0,0)[/tex] desse plano cartesiano, conforme mostra a próxima imagem.
Assim, para um cliente não pagar frete, as coordenadas do ponto [tex](x,y)[/tex] que correspondem à sua localização devem satisfazer a condição [tex]x^2+y^2\le 30^2[/tex], o que equivale a dizer que o ponto [tex](x,y)[/tex] está no disco de raio [tex]30[/tex] e centro [tex](0,0)[/tex].
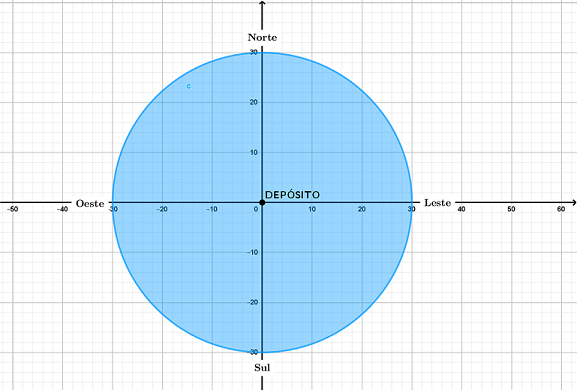
(a) Seja [tex]P=(x_P,y_P)[/tex] o ponto correspondente à localização da residência do cliente em questão.
- Como a residência está [tex]25\ km[/tex] a oeste do depósito, podemos considerar [tex]x_P=-25[/tex]. Assim, a localização desse cliente corresponde a um ponto da reta vertical [tex]r[/tex] destacada em roxo na próxima figura.
- Por outro lado, a localização do cliente fica ao sul do depósito e isso significa que [tex]y_P[/tex] é negativo.
- Observe que, para isenção do frete, a distância máxima, em linha reta, de um cliente ao depósito deve ser [tex]30 \, km[/tex]. Assim, o ponto que corresponde à localização no plano cartesiano do cliente em questão corresponde a um ponto da circunferência de raio [tex]30[/tex] e centro no ponto [tex](0,0).[/tex]
De posse dessas três informações, concluirmos que o maior valor para [tex]y[/tex] é obtido quando a localização da residência do cliente no plano cartesiano está na interseção da circunferência de raio [tex]30[/tex] com a reta [tex]r[/tex], ou seja, no ponto [tex]P[/tex] da figura a seguir.
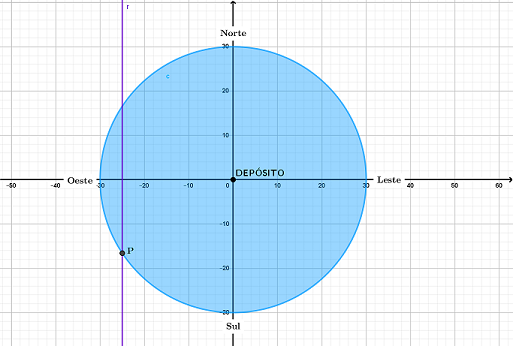
Veja que, algebricamente, obtemos os seguintes valores de [tex]y_P[/tex] para pontos localizados [tex]25\ km[/tex] a oeste, sobre a reta vertical [tex]x=-25 \, [/tex] e a [tex]30\ km[/tex] de distância do depósito:
[tex]\qquad (-25)^2+(y_P)^2= 30^2[/tex]
[tex]\qquad y_P^2= 900-625[/tex]
[tex]\qquad y_P^2= 275[/tex].
[tex]\qquad y_P =\pm 5\sqrt{11} [/tex].
Como estamos buscando o ponto que esteja [tex]y\ km[/tex] ao sul, o ponto [tex]P[/tex] tem coordenadas [tex](-25,-5\sqrt{11})[/tex], mas o valor máximo de [tex]y[/tex] é:
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$y = 5\sqrt{11}\ km \, $} \, .[/tex]
(b) Observe que a distância do ponto [tex](-25,-y)[/tex] ao depósito centrado na origem é dada por [tex]d=\sqrt{25^2+y^2}[/tex].
Como o custo é de [tex]R\$10,00[/tex] por quilômetro excedido de [tex] 30[/tex], temos que, para o consumidor em questão, a função custo definida para valores [tex] y \gt 5\sqrt{11}[/tex] é dada por:
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$C(y)=10\times(\sqrt{25^2+y^2}-30)$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Uma segunda solução para o item (a)
Se você ainda não aprendeu o que é um plano cartesiano, não faz mal, veja uma segunda solução para o item (a).
O consumidor em questão (C) reside [tex]25\ km[/tex] a oeste do depósito (D) e [tex] y \, km[/tex] ao sul, logo está a uma distância de
[tex]d=\sqrt{25^2+y^2}=\sqrt{625+y^2} \, km[/tex] do depósito,
conforme ilustra a figura a seguir.
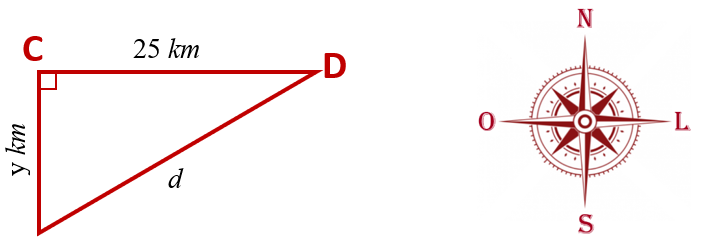
Como a empresa oferece frete gratuito para entregas do seu produto em um raio de até [tex]30\ km[/tex] do depósito, para que o consumidor C tenha isenção de frete é necessário [tex]d \leq 30[/tex]. Assim, segue que:
[tex]\qquad d \leq 30[/tex]
[tex]\qquad \sqrt{625+y^2} \leq 30[/tex]
[tex]\qquad 625+y^2 \leq 900[/tex]
[tex]\qquad y^2 \leq 900-625[/tex]
[tex]\qquad y^2 \leq 275[/tex]
e como [tex] y [/tex] é uma distância, temos que [tex]0 \leq y \leq 5\sqrt{11} [/tex].
Dessa forma, o valor máximo de [tex] y [/tex] para que o cliente tenha frete gratuito é [tex] \, \fcolorbox{black}{#eee0e5}{$y = 5\sqrt{11}\ km \, $} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
