Problema
(Indicado a partir do 9º ano do E. F.)
Três formigas estão paradas em três dos vértices de um retângulo no plano.
As formigas se movem uma por vez. A cada vez, a formiga que se move o faz segundo a reta paralela à determinada pelas posições das outras duas formigas.
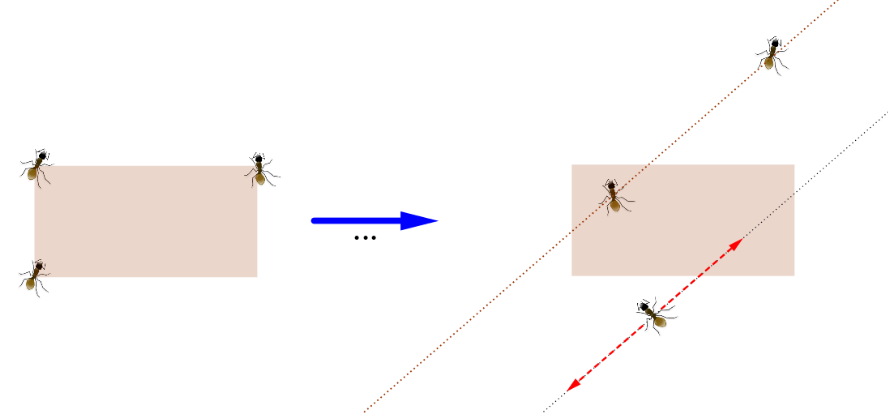
É possível que, após alguns movimentos, as formigas se situem nos pontos médios de três dos lados do retângulo original?
Fato que ajuda
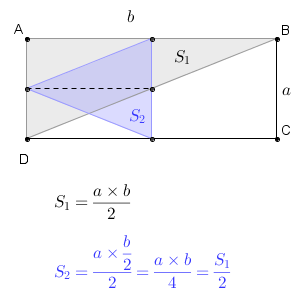
A justificativa desse fato é trivial, já que a própria definição da área de um triângulo, [tex]\dfrac{base \times altura}{2}[/tex], assegura a verdade da afirmação. Mas, se você precisar, utilize o applet abaixo para observar vários exemplos desse resultado.
Instruções:
1) Aguarde o arquivo carregar.
2) Observe que no applet aparece um triângulo inicial [tex]ABC[/tex], com base e altura pré-definidas. Você pode movimentar o ponto [tex]C[/tex] para obter outros triângulos com essas mesmas características e observar que as áreas dos triângulos obtidos são iguais.
3) Movimente os pontos [tex]A \, [/tex] e [tex] \, B[/tex] para definir outros triângulos iniciais [tex]ABC[/tex]. Para cada triângulo inicial definido, movimente o [tex]C[/tex] para obter outros triângulos com bases e alturas com os respectivos comprimentos iguais e observar, quantas vezes você quiser, que todos os triângulos obtidos têm a mesma área.
4) É importante lembrar que o GeoGebra fornece valores aproximados para as medidas apresentadas.
OBMEP_ srdg, criado com o GeoGebra
Solução
Não é possível!
Veja que, após o movimento de qualquer uma das formigas, a área do triângulo formado por suas posições não se altera.
Assim, após uma quantidade finita de movimentos, a área do triângulo formado pelas posições das formigas é igual à área do triângulo original, que por sua vez mede metade da área do retângulo original.
Como a área de um triângulo formado pelos pontos médios de três dos lados do retângulo [tex]ABCD[/tex] é igual a ¼ da área do mesmo, a situação descrita no enunciado não pode ocorrer.
Solução elaborada pelos Moderadores do Blog.
