Problema
(Indicado a partir do 3º ano do E. M.)
Qual o raio da esfera inscrita num tetraedro regular de aresta a ?
Lembretes
✐ Volume de uma pirâmide qualquer:
[tex]\qquad V_p=\dfrac{\text{Área da base}\times \text{Altura}}{3}=\dfrac{1}3\times \text{Área da base}\times \text{Altura}~.[/tex]
| ✐ Volume de uma pirâmide triangular (tetraedro), cuja base é um triângulo equilátero: [tex]\qquad V_t=\dfrac{1}3\times \text{Área da base}\times \text{Altura}\\ \qquad V_t=\dfrac{1}{3} \times \dfrac{a^2 \sqrt{3}}{4} \times h~.[/tex] |
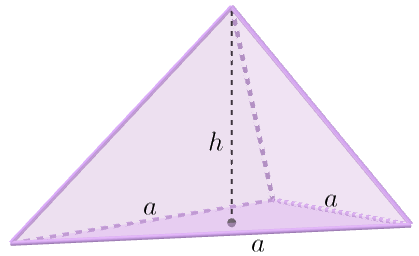 |
| ✐ Volume de um tetraedro regular: [tex]\qquad V_{tr}=\dfrac{1}{3} \times \dfrac{a^2 \sqrt{3}}{4} \times h\\ \qquad V_{tr}=\dfrac{1}{3} \times \dfrac{a^2 \sqrt{3}}{4} \times \left(\dfrac{a\, \sqrt{6}}{3} \right)\\ \qquad V_{tr}=\dfrac{1}{3} \times \dfrac{a^3 \sqrt{2}}{4}\\ \qquad V_{tr}=\dfrac{a^3 \sqrt{2}}{12}~.[/tex] |
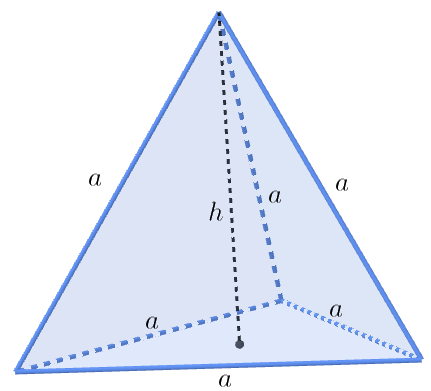 |
Solução
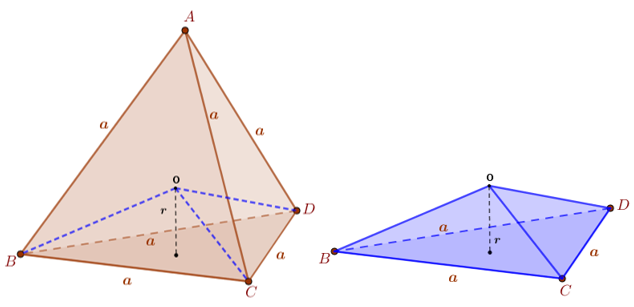
Consideremos o tetraedro regular [tex]ABCD[/tex] exibido na imagem a seguir, juntamente com esfera nele inscrita cujo centro é o ponto [tex]O[/tex] e cujo raio mede [tex]r[/tex].
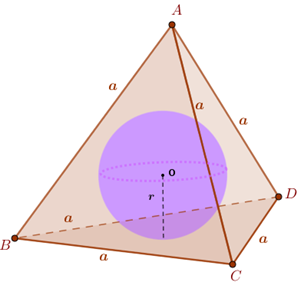
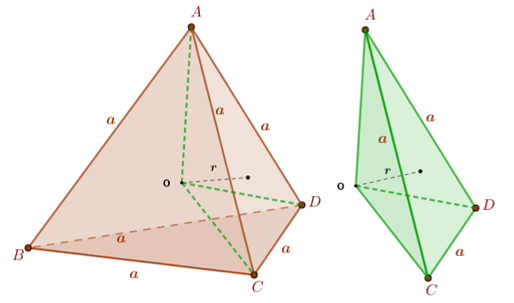
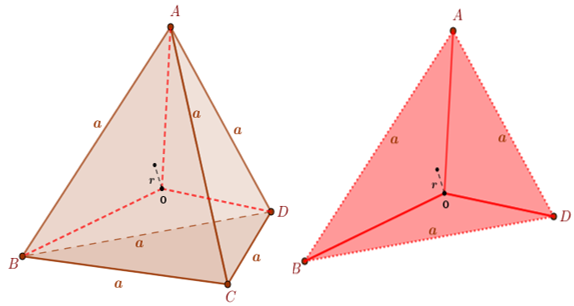
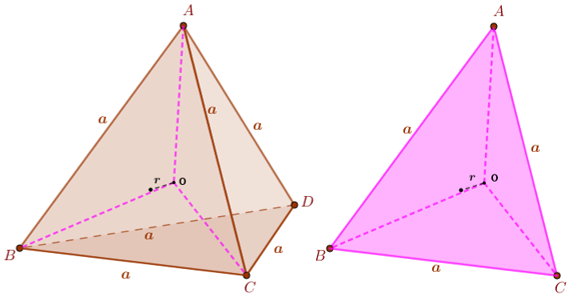
Se traçarmos segmentos com extremidades no centro da esfera e nos vértices do tetraedro, dividiremos o tetraedro [tex]ABCD[/tex] em quatro tetraedros que possuem como base um triângulo equilátero de lado [tex]a[/tex] e como altura o raio [tex]r[/tex] da esfera.
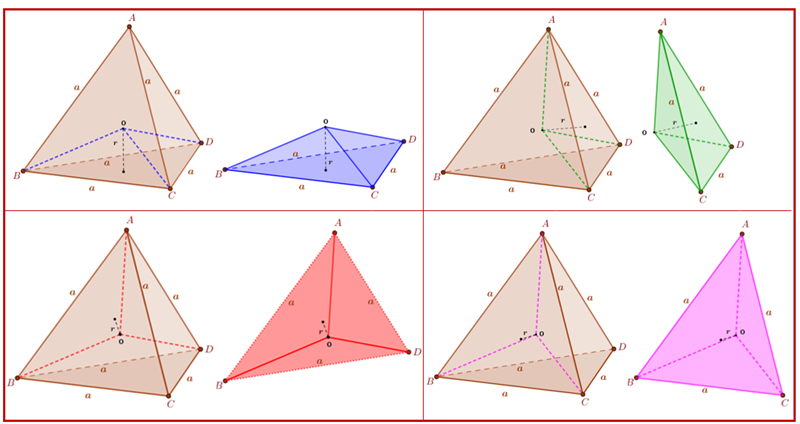
Como a soma dos volumes dos tetraedros originados é igual ao volume do tetraedro inicial, segue que:
[tex]\qquad 4 \cdot V_t=V_{tr}\\
\qquad 4 \cdot \dfrac{1}{3} \cdot \dfrac{a^2 \sqrt{3}}{4} \cdot r = \dfrac{a^3 \sqrt{2}}{12}\\
\qquad r = \dfrac{a^3 \sqrt{2}}{12} \cdot \dfrac{3}{a^2 \sqrt{3}}\\
\qquad \boxed{r = \dfrac{a \sqrt{6}}{12}~}\,.[/tex]
Para visualizar em tamanho maior os quatro tetraedros construídos a partir do centro da esfera inscrita, clique no botão abaixo.
Solução elaborada pelos Moderadores do Blog.