Problema
(Indicado a partir do 6º ano do E. F.)
(a) São dadas 4 moedas dentre as quais duas são falsas e as demais são legítimas. As moedas legítimas têm o mesmo peso. As falsas também têm o mesmo peso e são mais leves que as legítimas. Encontre as duas moedas falsas utilizando uma balança de pratos e realizando no máximo 2 pesagens.
(b) São dadas 7 moedas dentre as quais duas são falsas e as demais são legítimas. As moedas legítimas têm o mesmo peso. As falsas também têm o mesmo peso e são mais leves que as legítimas. Encontre as duas moedas falsas utilizando uma balança de pratos e realizando no máximo 3 pesagens.
Observação: Uma balança de pratos funciona da seguinte forma: caso você ponha um objeto no prato da esquerda que seja mais pesado que o objeto do prato da direita, o lado esquerdo ficará mais baixo que o lado da direita. Caso os objetos sejam de pesos iguais, a balança ficará em equilíbrio, ou seja, não haverá nenhum movimento dos pratos.
Solução 1
Quando escrevermos “pese tais coisas E tais coisas”, este E maiúsculo indicará a separação dos pratos. Por exemplo, “pese a moeda [tex]1[/tex] E a moeda [tex]4[/tex]” indicará que queremos colocar a moeda [tex]1[/tex] em um prato e a moeda [tex]4[/tex] no outro.
Se em alguma pesagem não houver equilíbrio entre os pratos, chamaremos de [tex]P+[/tex] o prato que “desceu” e de [tex]P-[/tex] o prato que “subiu”.
Também chamaremos as moedas de [tex]F[/tex] (falsas) ou [tex]V[/tex] (verdadeiras).
Usaremos, ainda, a notação (np) para indicar a n-ésima pesagem.
(a) Numere as moedas de [tex]1[/tex] a [tex]4[/tex]. Pese as moedas [tex]1[/tex] E [tex]2[/tex] (1p). Podem acontecer duas situações nesta primeira pesagem:
Situação 1: Se houver equilíbrio, as duas são [tex]F[/tex] ou as duas são [tex]V[/tex]. Neste caso, pese as moedas [tex]1[/tex] E [tex]3[/tex] (2p).
- Se a moeda [tex]1[/tex] ficar no [tex]P+[/tex], as moedas [tex]1,2[/tex] são [tex]V[/tex] e as moedas [tex]3,4[/tex] são [tex]F[/tex].
- Se a moeda [tex]1[/tex] ficar no [tex]P-[/tex], as moedas [tex]1,2[/tex] são [tex]F[/tex] e as moedas [tex]3,4[/tex] são [tex]V[/tex].
Situação 2: Se não houver equilíbrio, a moeda que ficar no [tex]P+[/tex] é [tex]V[/tex] e a que ficar no [tex]P-[/tex] é [tex]F[/tex]. Haverá uma verdadeira e uma falsa entre as outras duas moedas, bastando compará-las na (2p).
(b) Numere as moedas de [tex]1[/tex] a [tex]7[/tex]. Pese as moedas [tex]1,2,3[/tex] E [tex]4,5,6[/tex] (1p) (note que há pelo menos uma [tex]F[/tex] entre estas seis moedas!). As possíveis situações na primeira pesagem são:
Situação 1: Se houver equilíbrio, há uma [tex]F[/tex] em cada prato. Pese [tex]1[/tex] E [tex]2[/tex] (2p).
- Se houver equilíbrio, a moeda [tex]3[/tex] é [tex]F[/tex].
- Se não houver equilíbrio, a moeda [tex]F[/tex] é a do [tex]P-[/tex] desta última pesagem.
- Realize procedimento análogo com as moedas [tex]4[/tex] E [tex]5[/tex] (3p): Se houver equilíbrio, a moeda [tex]6[/tex] é [tex]F[/tex]; se não houver equilíbrio, a moeda [tex]F[/tex] é a do [tex]P-[/tex] desta última pesagem.
Situação 2: Se não houver equilíbrio, a moeda [tex]7[/tex] é [tex]F[/tex] ou há duas [tex]F[/tex] entre as moedas do [tex]P-[/tex]. Para descobrir em qual caso estamos, troque a moeda [tex]7[/tex] por alguma do [tex]P+[/tex] (2p) (note que só há moedas [tex]V[/tex] no [tex]P+[/tex]).
- Se houver equilíbrio, a moeda [tex]7[/tex] é [tex]F[/tex] e a moeda [tex]F[/tex] do outro prato pode ser descoberta na (3p) através do método já exposto para encontrar uma [tex]F[/tex] entre três moedas.
- Se o equilíbrio continuar inexistindo, há duas moedas [tex]F[/tex] no prato [tex]P-[/tex]. Basta tomar duas moedas de [tex]P-[/tex] e pesar (3p).
- Se equilibrarem, as duas são [tex]F[/tex].
- Se não equilibrarem, as [tex]F[/tex] são a que ficou, agora, no prato [tex]P-[/tex], e a que não foi utilizada nesta última pesagem.
Esses procedimentos estão ilustrados na figura que se segue. Considere que:
– as setas a partir de um prato sugerem como proceder na pesagem seguinte no caso desse prato descer;
– as setas a partir do ponto da base da balança sugerem como proceder na pesagem seguinte no caso de equilíbrio dos pratos.
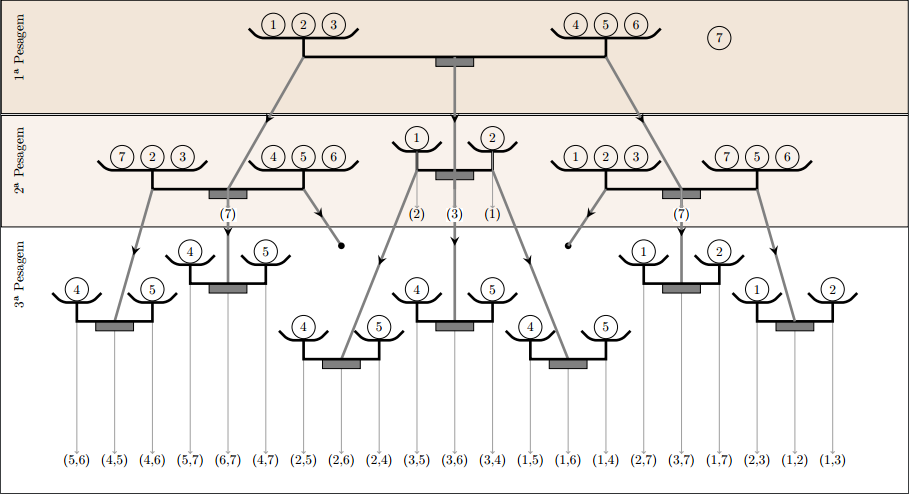
Solução elaborada pelos Moderadores do Blog.
Solução 2
(item a)
(a) Têm-se 4 moedas, onde 2 são falsas e 2 legítimas, as legítimas têm o mesmo peso e são mais pesadas que as falsas, que também têm o mesmo peso.
Antes de se fazer qualquer pesagem, pode-se perceber que se forem postas uma moeda de cada lado e a balança ficar em equilíbrio, estas têm o mesmo peso, ou seja, as duas são falsas ou verdadeiras. Assim, para se identificar as duas moedas falsas, dentre as quatro, com apenas duas pesagens, é necessário que a primeira seja realizada com uma moeda de cada lado. A partir daí, pode ocorrer que a balança fique em equilíbrio, ou não.
- Supondo o 1º caso, onde a balança esteja equilibrada, ali haverá duas moedas do mesmo tipo, verdadeiras ou falsas. Para a distinção das duas, se retira uma e a separa, e em seu lugar se põe uma das duas que estiveram fora da balança, realizando a segunda pesagem. Necessariamente, nesta pesagem a balança não se equilibrará, nota-se então o movimento do prato onde estava a moeda da primeira pesagem, se ele subiu, a moeda que está ali é falsa pois é mais leve que a outra e consequentemente a moeda que foi retirada e separada após a 1º pesagem também não é uma das verdadeiras. Mas, se o mesmo prato descer, aquela moeda será verdadeira, e a outra separada também.
- Suponha agora o 2º caso, onde a balança estará em desequilíbrio com uma moeda em cada prato. Será notório que ali haverá uma verdadeira e uma falsa; portanto se realiza a segunda pesagem para fazermos a distinção entre as duas moedas que não foram utilizadas nesta pesagem. Pode-se substituir a moeda mais pesada, ou seja legítima, por outra. Se nesta segunda pesagem a balança equilibrar as duas que estão nela são as falsas. Mas se ela desequilibrar novamente a moeda que não foi posta na balança ainda será falsa, junto com a que não foi retirada do prato na 1º pesagem. Da mesma maneira, pode-se retirar a moeda mais leve, e fazer a distinção de maneira semelhante.
Solução elaborada pelo COM Águias da Matemátika, com contribuições dos Moderadores do Blog.
