.Problemão: Distância entre o Sol e corpos celestes (S)

Problema
(Indicado a partir do 1º ano do E. M.)

---

(OPM, Nível Gama – Adaptado) A distância [tex]d[/tex] do Sol a um corpo celeste que gira em torno dele, como o planeta Terra, pode ser dada por
[tex]\qquad \qquad d = \dfrac{a(1-e^2)}{1-e\cos\;\theta}[/tex],
onde
[tex]\quad a[/tex] é a distância média em unidades astronômicas,
[tex]\quad e[/tex] é uma constante chamada excentricidade e
[tex]\quad\theta[/tex] é um ângulo entre [tex]0[/tex] e [tex]360^{\circ}[/tex] (veja a figura abaixo).
As constantes [tex]a[/tex] e [tex]e[/tex] são fornecidas na tabela a seguir para cada planeta e também para Plutão.

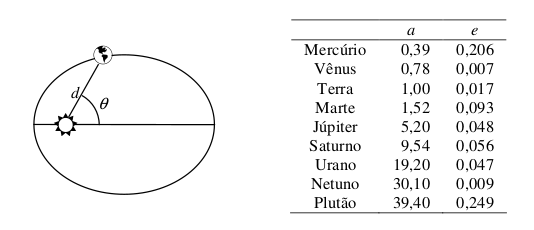
a) Encontre expressões em termos de [tex]a[/tex] e [tex]e[/tex] que representem a distância mínima e máxima de cada planeta e de Plutão até o Sol.
b) Plutão está sempre mais distante do Sol do que Netuno?

Solução

---

a) Observe a seguinte sequência de expressões equivalentes:

[tex]\qquad \begin{align}
-1\leq \cos\;\theta\leq 1 &\iff -e\leq e\cos\;\theta\leq e\\
&\iff -e\leq -e\cos\;\theta\leq e\\
&\iff 0<1-e\leq 1-e\cos\;\theta\leq 1+e\\ &\iff \dfrac{a}{1+e}\leq \dfrac{a}{1-e\cos\;\theta}\leq \dfrac{a}{1-e}\\ &\iff \dfrac{a(1-e^2)}{1+e}\leq \dfrac{a(1-e^2)}{1-e\cos\;\theta}\leq \dfrac{a(1-e^2)}{1-e}\\ &\iff a(1-e)\leq d\leq a(1+e). \end{align}[/tex]

Assim:

• a distância mínima de Plutão e qualquer planeta ao Sol é de [tex]\,\boxed{a(1-e)}\,[/tex] unidades astronômicas,
• a distância máxima de Plutão e qualquer planeta ao Sol é de [tex]\,\boxed{a(1+e)}\,[/tex] unidades astronômicas.

b) Pelo item anterior e pela tabela fornecida, a distância mínima de Plutão ao Sol é
[tex]\qquad a(1-e) = 39,40\cdot (1-0,249) = 29,5894[/tex] unidades astronômicas,
enquanto que a distância mínima de Netuno ao Sol é
[tex]\qquad a(1-e) = 30,10\cdot(1-0,009) = 29,8291[/tex] unidades astronômicas.

Portanto, quando Plutão estiver o mais próximo possível do Sol, ele estará mais próximo do que Netuno.

---

Solução elaborada pelos Moderadores do Blog.