Problema
(Indicado a partir do 2º ano do E. M.)
(Mackenzie-SP, 2008 – Adaptado) Na figura, o quadrado ABCD é formado por 9 quadrados congruentes.
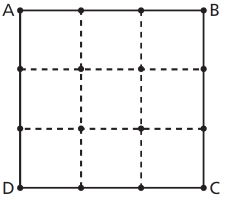
Determine a quantidade de triângulos distintos que podem ser construídos a partir dos 16 pontos.
Solução
Um triângulo é definido por três pontos (não colineares). Assim, precisamos determinar a quantidade de maneiras de selecionarmos três pontos não colineares no quadrado ABCD.
Repare que o total de agrupamentos de 3 pontos é dado por [tex]C_{16}^3 = 560[/tex], incluídos os agrupamentos com pontos colineares.
Agora vamos calcular o total de agrupamentos com três pontos colineares:
Existem 4 linhas, 4 colunas e 2 diagonais, cada uma com 4 pontos colineares. Cada uma dessas gera um total de [tex]C_4^3 = 4[/tex] agrupamentos de três pontos colineares. Logo, contabilizamos [tex]10\times 4 = 40[/tex] agrupamentos de três pontos colineares.
Existem ainda 4 diagonais com três pontos colineares cada (conforme figura abaixo), o que resulta em outros [tex]4[/tex] agrupamentos de três pontos colineares.
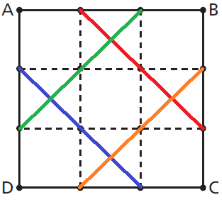
Portanto, o total de triângulos que podem ser construídos é de [tex]560-(40+4) = 516.[/tex]
Solução elaborada pelos Moderadores do Blog.
