Problema
(Indicado a partir do 9º ano do E. F.)
Uma usina comprou [tex]2000[/tex] litros de leite puro e então retirou certo volume [tex]V[/tex] desse leite para produção de iogurte, substituindo esse volume por água em igual quantidade. Em seguida, retirou novamente o mesmo volume [tex]V[/tex] da mistura e novamente substituiu por água em igual quantidade. Sabendo que na mistura final há exatamente [tex]1125[/tex] litros de leite, determine o valor de [tex]V[/tex].
Extraído da XXIV OBM.
Solução
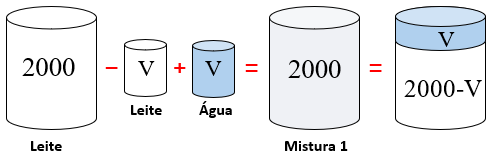
No início tínhamos [tex]2000[/tex] litros apenas de leite.
- Após a primeira retirada e o complemento com água, ficamos com [tex]\boxed{2000-V}[/tex] litros de leite e [tex]V[/tex] litros de água. Vamos supor que haverá uma mistura homogênea entre o leite e a água.
- Na segunda retirada de um volume [tex]V[/tex], não estaremos retirando apenas leite, mas a mistura de leite e água. Indicaremos por [tex]x[/tex] o volume de leite retirado neste segundo momento.
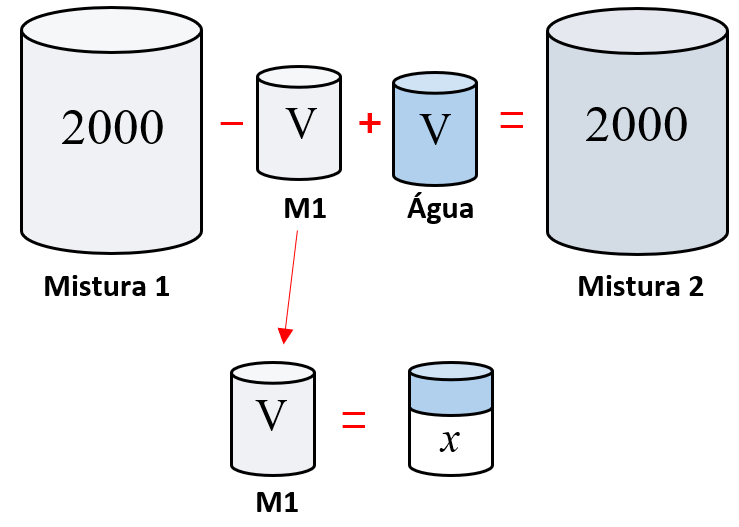
Como a mistura é homogênea, na segunda retirada a concentração de leite no volume [tex]V[/tex] extraído da mistura é igual à concentração de leite existente na mistura, ou seja:
[tex]\qquad \dfrac{x}{V} = \dfrac{2000-V}{2000}[/tex]
[tex]\qquad x =\boxed{\dfrac{2000\cdot V – V^2}{2000}}\;[/tex].
Assim, após a segunda retirada, restou apenas [tex]\boxed{(2000-V)-\dfrac{2000V-V^2}{2000}}[/tex] litros de leite.
Sabendo que na mistura final há exatamente [tex]1125[/tex] litros de leite, segue que
- [tex]\qquad (2000-V)-\dfrac{2000\cdot V-V^2}{2000}=1125[/tex]
[tex]\qquad \dfrac{2000\cdot (2000-V)-(2000\cdot V-V^2)}{2000}=1125[/tex]
[tex]\qquad \dfrac{2000\cdot (2000-V)-V\cdot (2000-V)}{2000}=1125[/tex]
[tex]\qquad \dfrac{(2000-V)\cdot (2000-V)}{2000}=1125[/tex]
[tex]\qquad \dfrac{(2000-V)^2}{2000}=1125[/tex]
[tex]\qquad (2000-V)^2=1125\cdot2000[/tex]
[tex]\qquad (2000-V)^2=2250000[/tex]
[tex]\qquad \sqrt{(2000-V)^2~}=\sqrt{2250000}[/tex]
[tex]\qquad \left|\;2000-V\;\right|=1500[/tex]
[tex]\qquad 2000- V =\pm 1500[/tex].
Como estamos lidando com quantidades de leite, então [tex]2000- V \ge 0[/tex] e assim [tex]\boxed{2000- V = 1500}[/tex].
Portanto, concluímos que [tex]\, \fcolorbox{black}{#eee0e5}{$V = 500\,\,litros$} \,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Participou da discussão do problema o Clube: Math Error.