✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
(Fuvest, 2019 – Adaptado) O cilindro de papelão central de uma fita crepe tem raio externo de [tex]3 \;cm[/tex]. A fita tem espessura de [tex]0,01 \;cm[/tex] e dá [tex]100[/tex] voltas completas.
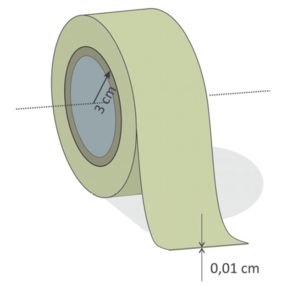
Considerando que, a cada volta, o raio externo do rolo é aumentado no valor da espessura da fita, encontre o comprimento aproximado da fita, em metros.

Lembretes e notações
[tex]\textcolor{#800000}{(1)}\;[/tex] Dada a PA [tex]\left(a_1,a_2,\cdots,a_n, \cdots\right)[/tex] de razão [tex]r[/tex], denotamos a soma de seus [tex]n[/tex] primeiros termos por
[tex]\qquad S_{n} = a_1 + a_2 + \dots + a_{n}[/tex].
Neste caso, valem as seguintes igualdades:
[tex]\textcolor{#800000}{(2)}\;[/tex] [tex]S_{n}= \dfrac{(a_{1}+a_{n} )\cdot n}{2}[/tex].
[tex]\textcolor{#800000}{(3)}\;[/tex] [tex]a_{n}=a_{1}+ (n-1)\cdot r[/tex].
Solução
- Vamos calcular, inicialmente, o comprimento [tex]C_n[/tex] de fita na [tex]n[/tex]-ésima volta dada:
1ª volta: [tex]C_1 = 2\cdot \pi \cdot 3 = 6\pi;[/tex]
2ª volta: [tex]C_2 = 2\cdot \pi \cdot 3,01 = 6,02\pi;[/tex]
3ª volta: [tex]C_3 = 2\cdot \pi \cdot 3,02 = 6,04\pi.[/tex]
Perceba que os comprimentos de fita nas várias voltas formam uma Progressão Aritmética com primeiro termo igual a [tex]6\pi[/tex] e razão igual a [tex]0,02\pi[/tex]. Assim, pelo Lembrete (3), o comprimento de fita na volta de número [tex]100[/tex] é
[tex]\qquad C_{100} = 6\pi+99\cdot 0,02\pi = 6\pi+1,98\pi = 7,98\pi.[/tex] - Para finalizar, observe que o comprimento total de fita, [tex]C[/tex], é dado pela seguinte soma:
[tex]\qquad C=C_1+C_2+~\cdots~+C_{100}\,;[/tex]
logo, pelo Lembrete (2), segue que:
[tex]\qquad C = 6\pi+6,02\pi+6,04\pi+\cdots+7,98\pi [/tex]
[tex]\qquad C = (6+6,02+6,04+\cdots+7,98)\pi[/tex]
[tex]\qquad C = \dfrac{(6+7,98)\cdot 100}{2}\cdot \pi[/tex]
[tex]\qquad C = (6+7,98)\cdot 50\cdot \pi[/tex]
[tex]\qquad C \approx 2196\;cm[/tex]
[tex]\qquad C \approx 22\;m.[/tex]
Solução elaborada pelos Moderadores do Blog.
