Problema
(Indicado a partir do 2º ano do E. M.)
Escrevem-se números de cinco dígitos (inclusive os começados por zero) em cartões. Com a fonte utilizada, os dígitos [tex]0[/tex], [tex]1[/tex] e [tex]8[/tex] não se alteram de cabeça para baixo, enquanto o dígito [tex]6[/tex] de cabeça para baixo se transforma em [tex]9[/tex]. Assim, um só cartão pode representar dois números (por exemplo, [tex]06198[/tex] e [tex]86190[/tex]). Qual é a quantidade mínima de cartões para representar todos os números de cinco dígitos?
(Extraído do livro Análise Combinatória e Probabilidade: Augusto César Morgado e outros.)
Solução
Inicialmente, observe que, utilizando os algarismos de [tex]0[/tex] a [tex]9[/tex], o Princípio Fundamental da Contagem nos garante que podem ser obtidos [tex]10 \times 10 \times 10 \times 10 \times 10 = 100000[/tex] números de cinco dígitos, incluindo os começados por zero. No entanto, na hora de escrever tais números, repare que existem três tipos de cartões:
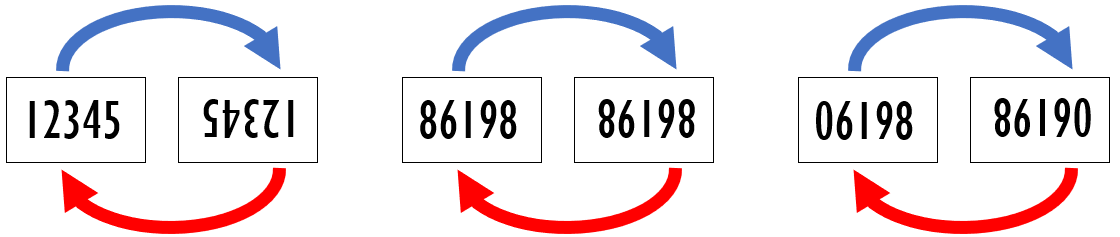
(I) Os que quando virados de cabeça para baixo não exibem números, como, por exemplo, [tex]12345[/tex];
(II) Os que quando virados de cabeça para baixo exibem o mesmo número, como, por exemplo, [tex]86198[/tex];
(III) Os que quando virados de cabeça para baixo exibem números diferentes, como, por exemplo, [tex]06198[/tex].
Agora, perceba que os cartões do tipo (III) permitem economia, pois um mesmo cartão desse tipo exibe dois números diferentes. Vamos obter a quantidade de cartões desse tipo.
Novamente, pelo Princípio Fundamental da Contagem, há [tex]5 \times 5 \times 5 \times 5 \times 5 = 3125[/tex] cartões que virados de cabeça para baixo exibem números, iguais ou diferentes, pois tais cartões possuem apenas os algarismos [tex]0[/tex], [tex]1[/tex], [tex]8[/tex], [tex]6[/tex] ou [tex]9[/tex].
Destes, [tex]5 \times 5 \times 3 = 75[/tex] são do segundo tipo, pois um desses cartões deve ter:
- as casas das extremidades preenchidas nas formas
- a segunda e a quarta casas preenchidas nas formas
- e a casa central preenchida por [tex]0[/tex], [tex]1[/tex] ou [tex]8[/tex].
[tex]\qquad 0\,\underline{\,}\,\underline{\,}\,\underline{\,}\,0[/tex];
[tex]\qquad 1\,\underline{\,}\,\underline{\,}\,\underline{\,}\,1[/tex];
[tex]\qquad 8\,\underline{\,}\,\underline{\,}\,\underline{\,}\,8[/tex];
[tex]\qquad 6\,\underline{\,}\,\underline{\,}\,\underline{\,}\,9[/tex] ou
[tex]\qquad 9\,\underline{\,}\,\underline{\,}\,\underline{\,}\,6[/tex],
[tex]\qquad \underline{\,}\,0\,\underline{\,}\,0\underline{\,}[/tex];
[tex]\qquad \underline{\,}\,1\,\underline{\,}\,1\,\underline{\,}\,[/tex];
[tex]\qquad \underline{\,}\,8\,\underline{\,}\,8\,\underline{\,}\,[/tex];
[tex]\qquad \underline{\,}\,6\,\underline{\,}\,9\,\underline{\,}\,[/tex] ou
[tex]\qquad \underline{\,}\,9\,\underline{\,}\,6\,\underline{\,}\,[/tex]
Portanto, a quantidade de cartões do tipo (III) é [tex]3125-75=3050[/tex] e, dessa forma, podem ser economizados [tex]\dfrac{3050}{2}=1525[/tex] cartões.
Pelo exposto, concluímos que o número mínimo de cartões necessário para representar todos os números de cinco dígitos é [tex]100000-1525= \, \fcolorbox{black}{#eee0e5}{$98475$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
