Problema
(Indicado a partir do 2º ano do E. M.)
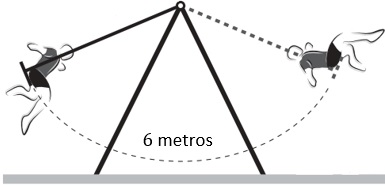
Depois de percorrer um comprimento de arco de [tex]6[/tex] metros, uma criança deixa de empurrar o balanço em que está brincando. Se o atrito diminui a velocidade do balanço de modo que o comprimento de arco percorrido seja sempre igual a [tex]80\%[/tex] do anterior, calcule a distância total percorrida pela criança, em metros, até que o balanço pare completamente.
Solução
Vamos escrever a distância, em metros, percorrida em cada movimento:
[tex]\qquad 1°[/tex] movimento[tex]\rightarrow[/tex] [tex]6[/tex];
[tex]\qquad 2°[/tex] movimento[tex]\rightarrow[/tex] [tex](0,8)\times6[/tex];
[tex]\qquad 3°[/tex] movimento[tex]\rightarrow[/tex] [tex](0,8)^2\times6[/tex];
[tex]\qquad 4°[/tex] movimento[tex]\rightarrow[/tex] [tex](0,8)^3\times6[/tex];
[tex]\qquad \vdots[/tex]
Estamos procurando a distância total percorrida, ou seja:
[tex]\qquad \boxed{S=6 + (0,8)\times6 + (0,8)^2\times6 + (0,8)^3\times6 + \cdots}[/tex].
Essa distância [tex]S[/tex] é o limite da soma de uma progressão geométrica e pode ser calculada pela fórmula
[tex]\qquad S=\dfrac{a_1}{1-q}[/tex],
na qual, no nosso caso, [tex]a_1[/tex] seria o último comprimento de arco percorrido antes de a criança deixar de empurrar o balanço ([tex]a_2[/tex] seria o primeiro comprimento de arco percorrido após a criança deixar de empurrar o balanço) e [tex]q[/tex] seria [tex]80\%[/tex]
Assim:
[tex]\qquad S=\dfrac{6}{1-0,8}=30 \, m.[/tex]
Correto?
Nem tanto. Obviamente, há um problema aqui, pois é absurdo conceber que a criança balançará infinitas vezes. Na vida real, algumas ações físicas impossibilitarão esta situação. Portanto, a resposta encontrada é apenas uma aproximação.
Solução elaborada pelos Moderadores do Blog.
