Problema
(Indicado a partir do 9º ano do E. F.)
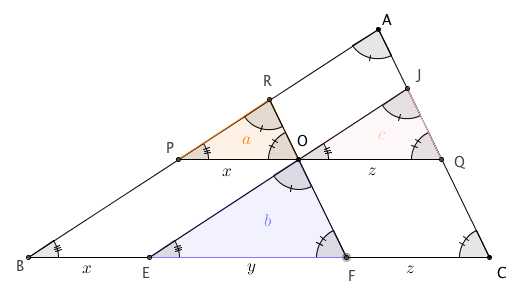
Considerando um triângulo ABC, traçam-se por um ponto interno O três paralelas a seus lados e obtém-se três triângulos menores de áreas [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex], conforme figura abaixo.
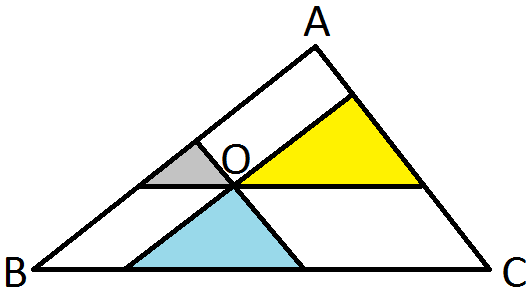
Mostre que a área do triângulo ABC é dada por [tex](\sqrt{a}+\sqrt{b}+\sqrt{c})^2[/tex].
Ferramentas que ajudam
Para resolvermos este problema, vamos relembrar algumas propriedades.
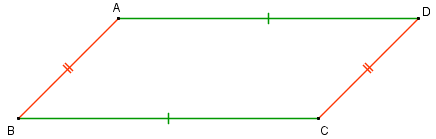
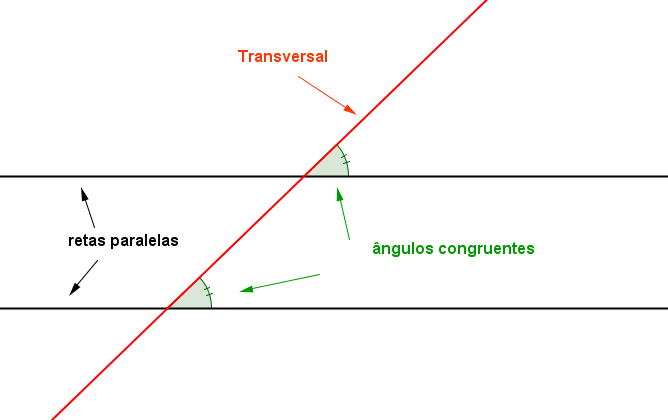
Reta transversal a outras retas é uma reta que intersecta essas outras retas em pontos diferentes.
Alguns autores chamam este Caso de Semelhança de caso A.A.A. De fato, uma vez que a soma dos ângulos internos de um triângulo é sempre [tex]180^\circ[/tex] (Lei Angular de Tales), se entre dois triângulos há uma correspondência entre dois pares de ângulos, também haverá uma correspondência entre o terceiro par. Assim, o caso (ângulo – ângulo) também pode ser visto como caso (ângulo – ângulo – ângulo).
Solução
Pois bem, vamos à solução.
Na figura abaixo, considere os segmentos de comprimentos [tex]x[/tex], [tex]y[/tex] e [tex]z[/tex] na base BC do triângulo ABC. Note que [tex]PO=x[/tex] e [tex]OQ=z[/tex], pela propriedade [tex]1[/tex], já que os quadriláteros PBEO e OFCQ são paralelogramos.
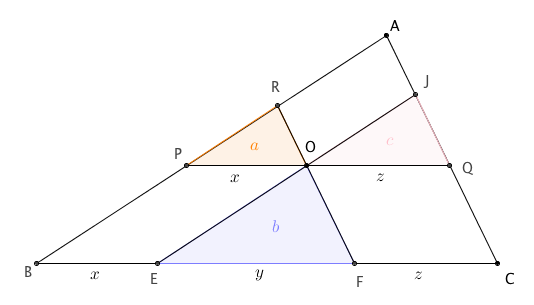
Pelo caso de semelhança A.A.A. (propriedade [tex]3[/tex]), os três triângulos menores formados quando são traçadas as paralelas aos lados de ABC são semelhantes ao triângulo ABC, pois, pela propriedade [tex]2[/tex] usada repetidas vezes, as medidas dos ângulos internos dos triângulos menores corresponderão às medidas dos ângulos internos do triângulo ABC.
Assim, denotando por [tex]S'[/tex] a área do triângulo ABC, podemos escrever a seguinte relação entre as áreas, advinda da semelhança entre os triângulos RPO e ABC, cuja razão é [tex]\dfrac{x}{x+y+z}[/tex], e da utilização da Propriedade [tex]4[/tex]:
[tex]\qquad \dfrac{a}{S’}=\left(\dfrac{x}{x+y+z}\right)^2[/tex],
donde
[tex]\qquad \dfrac{\sqrt{a}}{\sqrt{S’}}=\dfrac{x}{x+y+z}. \qquad \qquad (I)[/tex]
Analogamente, temos:
[tex]\qquad \dfrac{\sqrt{b}}{\sqrt{S’}}=\dfrac{y}{x+y+z} \qquad (II)[/tex]
e
[tex]\qquad \dfrac{\sqrt{c}}{\sqrt{S’}}=\dfrac{z}{x+y+z}. \qquad (III)[/tex]
Somando [tex](I),\ (II), \ (III)[/tex], obtemos:
[tex]\qquad \dfrac{\sqrt{a}}{\sqrt{S’}}+\dfrac{\sqrt{b}}{\sqrt{S’}}+\dfrac{\sqrt{c}}{\sqrt{S’}}=\dfrac{x+y+z}{x+y+z}=1[/tex],
ou seja,
[tex]\qquad \dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{S’}}=1[/tex].
Assim,
[tex]\qquad \sqrt{S’}=\sqrt{a}+\sqrt{b}+\sqrt{c}[/tex]
e, finalmente,
[tex]\qquad \boxed{S’=\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2}[/tex].
Solução elaborada pelos Moderadores do Blog.
