Problema
(Indicado a partir do 9º ano do E. F.)
Na figura, [tex]ABCD[/tex] é um quadrado de lado com comprimento [tex]a[/tex] e temos dois arcos de circunferências com centros nos pontos [tex]A[/tex] e [tex]B[/tex].
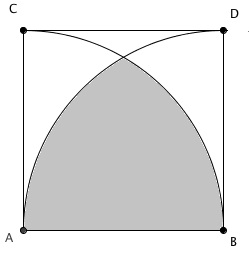
Calcule a área da região sombreada em função de [tex]a[/tex].
Solução
Seja [tex]E[/tex] a interseção dos dois arcos; temos, então, que [tex]AB = AE = BE = a[/tex].
Assim, [tex]\Delta ABE[/tex] é um triângulo equilátero de lado [tex]a[/tex] e, portanto, as medidas dos ângulos [tex]A\hat{B}E [/tex] e [tex]B\hat{A}E[/tex] são ambas [tex]60^{\circ}[/tex].
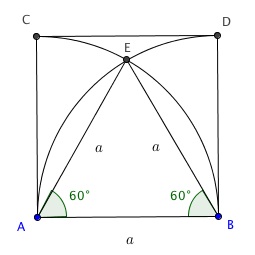
Podemos, então, considerar que a região em destaque é a união de dois setores circulares de [tex]60^{\circ}[/tex] com raio [tex]a[/tex].
Poderíamos, a princípio, pensar que a região em questão seria equivalente a um setor circular de [tex]120^{\circ}[/tex] com raio [tex]a[/tex], cuja área corresponde à área de um terço de um círculo de raio [tex]a[/tex]. Entretanto, deste modo estaremos contando a região limitada pelo triângulo [tex]\Delta ABE[/tex] duas vezes, e, neste caso, precisamos descontar uma região triangular.
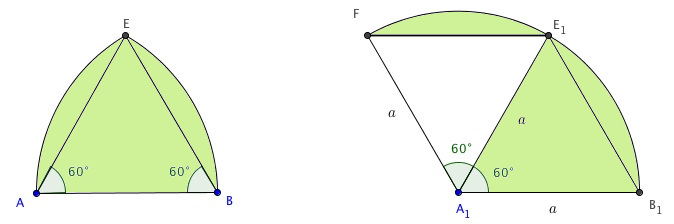
Portanto, a área [tex]S[/tex] da região em destaque pode ser calculada como [tex]S=S_1-S_2[/tex], onde:
- [tex]S_1[/tex] corresponde a um terço da área de um círculo de raio [tex]a[/tex];
- [tex]S_2[/tex] corresponde à área de um triângulo equilátero de lados com comprimentos [tex]a[/tex].
Vamos aos cálculos.
Como
[tex]\qquad \boxed{S_1=\dfrac{\pi\cdot a^2}{3}}[/tex]
e
[tex]\qquad S_2=\dfrac{\text{base}\times\text{altura}}{2}\\
\qquad S_2=\dfrac{a\times \left(a \times \text{sen}\,60^\circ\right)}{2}\\
\qquad S_2=\dfrac{a\times \left(a \times \dfrac{\sqrt{3~}}{2}\right)}{2}[/tex]
[tex]\qquad \boxed{S_2=\dfrac{a^2 \,\sqrt{3}}{4}}[/tex],
segue que:
[tex]\qquad S=S_1-S_2\\
\qquad S=\dfrac{\pi \cdot a^2}{3}-\dfrac{a^2\, \sqrt{3}}{4}\\
\qquad \fcolorbox{black}{#eee0e5}{$S=\dfrac{ 4\pi-3\sqrt{3}}{12}~a^2$}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
