Problema
(Indicado a partir do 9º ano do E. F.)
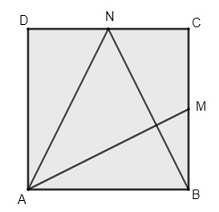
(Extraído do livro Temas e Problemas Elementares) Considere o quadrado formado pelos pontos [tex]A[/tex], [tex]B[/tex], [tex]C[/tex] e [tex]D[/tex], com lados medindo [tex]10\;cm[/tex]. Sejam [tex]M[/tex] e [tex]N[/tex] os pontos médios dos lados [tex]\overline{BC}[/tex] e [tex]\overline{CD}[/tex], respectivamente. Construindo os segmentos [tex]\overline{AM}[/tex], [tex]\overline{AN}[/tex] e [tex]\overline{NB}[/tex], dividimos o quadrado em cinco partes, como na figura.
Determine a área de cada uma dessas partes.

Lembrete
Se dois triângulos possuem a mesma altura, então a razão entre as medidas de suas áreas é igual à razão entre as medidas de suas bases, relativas a essa altura.
Notação
- Denotaremos o segmento definido pelos pontos, digamos, [tex]X[/tex] e [tex]Y[/tex] por [tex]\overline{XY}[/tex], e o seu comprimento por [tex]XY[/tex].
- O triângulo formado pelos pontos, digamos, [tex]X[/tex], [tex]Y[/tex] e [tex]Z[/tex] será denotado por [tex]\Delta(XYZ)[/tex].
Solução
Consideremos [tex]F[/tex] o ponto médio do lado [tex]\overline{AB}[/tex] e [tex]P[/tex] o ponto de interseção dos segmentos [tex]\overline{AM}[/tex] e [tex]\overline{NB}[/tex]. Traçando o segmento [tex]\overline{NF}[/tex] obtemos o ponto [tex]Q[/tex], interseção dos segmentos [tex]\overline{AM}[/tex] e [tex]\overline{NF}[/tex]. Com essas considerações obtemos a [tex]\textbf{Figura 1}[/tex] abaixo.
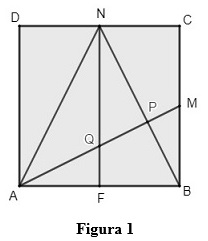
- Notemos que os triângulos [tex]\Delta(ABM)[/tex] e [tex]\Delta(AFQ)[/tex] são semelhantes, uma vez que seus lados são paralelos e, consequentemente, seus ângulos internos são congruentes. Assim, [tex] \dfrac{AB}{AF}=\dfrac{BM}{FQ}[/tex], donde:
- Da mesma forma, os triângulos [tex]\Delta(NPQ)[/tex] e [tex]\Delta(BPM)[/tex] são semelhantes, então:
- Novamente, utilizando os triângulos semelhantes [tex]\Delta(ABM)[/tex] e [tex]\Delta(AFQ)[/tex] temos que
[tex]\qquad \dfrac{10}{5}=\dfrac{5}{FQ}\\\
\qquad FQ=2,5\;cm. [/tex]
Como [tex]NF=10\;cm[/tex], temos que [tex]NQ=10-FQ [/tex] e assim:
[tex]\qquad NQ=10-2,5\\
\qquad NQ=7,5\;cm.[/tex]
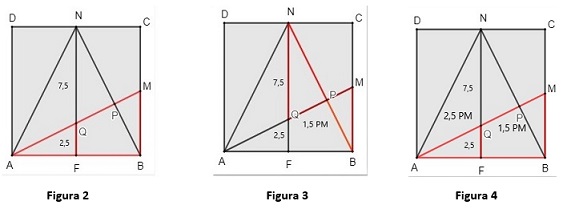
Na [tex]\textbf{Figura 2}[/tex], ilustramos as medidas dos segmentos [tex]\overline{FQ}[/tex] e [tex]\overline{NQ}[/tex].
[tex]\qquad \dfrac{NQ}{BM}=\dfrac{PQ}{PM}\\
\qquad \dfrac{7,5}{5}=\dfrac{PQ}{PM}\\
\qquad PQ=1,5PM.[/tex]
Na [tex]\textbf{Figura 3}[/tex], acima, ilustramos o segmento [tex]\overline{PQ}[/tex], juntamente com os que já foram obtidos.
[tex] \qquad \dfrac{AM}{AQ}=\dfrac{BM}{FQ} \\
\qquad \dfrac{AM}{AQ}=\dfrac{5}{2,5}\\
\qquad \dfrac{AM}{AQ}=2\\
\qquad AM=2AQ.[/tex]
Sendo [tex]AM=AQ+QP+PM[/tex] resulta que
[tex]\qquad AQ+1,5PM+PM=2AQ\\
\qquad AQ=2,5 PM.[/tex]
Na [tex]\textbf{Figura 4}[/tex], ilustramos a medida do segmento [tex]\overline{AQ}[/tex], bem como as demais medidas obtidas.
Uma vez que o quadrado tem lado medindo [tex]10\;cm[/tex], a área, [tex]A_1[/tex], do triângulo retângulo [tex]\Delta(ABM)[/tex] é dada por
\begin{equation} A_1=\dfrac{1}{2}(BM\times AB)=\dfrac{1}{2}(5\times 10)= 25\;cm^2.\end{equation}
Observemos que as alturas dos triângulos [tex]\Delta(ABM)[/tex] e [tex]\Delta(ABP)[/tex], em relação às bases [tex]\overline{AM}[/tex] e [tex]\overline{AP}[/tex], respectivamente, são iguais. Denotando por [tex]A_2[/tex] a área do triângulo do [tex]\Delta(ABP)[/tex], pelo Lembrete, temos que:
[tex]\qquad \dfrac{A_1}{A_2}=\dfrac{AM}{AP}\\
\qquad \dfrac{25}{A_2}=\dfrac{2AQ}{AQ+QP}\\
\qquad \dfrac{25}{A_2}=\dfrac{2(2,5PM)}{2,5PM+1,5PM}\\
\qquad \dfrac{25}{A_2}=\dfrac{5\cancel{PM}}{4\cancel{PM}}. [/tex]
Assim, a área do triângulo [tex]\Delta(ABP)[/tex] é [tex]A_2=20\;cm^2[/tex].
Com isso, conseguimos calcular a área [tex]A_3[/tex] do triângulo [tex]\Delta(BPM)[/tex]:
\begin{equation} A_3=A_1-A_2=25-20=5\;cm^2.\end{equation}
Notemos que os triângulos [tex]\Delta(ABM)[/tex], [tex]\Delta(ADN)[/tex] e [tex]\Delta(BCN)[/tex] são congruentes; assim, suas áreas possuem mesma medida, ou seja, todas valem [tex]A_1=25\;cm^2[/tex]. Dessa maneira, a área, [tex]A_4[/tex], do quadrilátero formado pelos pontos [tex]M,\;P,\;N[/tex] e [tex]C[/tex] é dada por
\begin{equation}
A_4=A_1-A_3=25-5=20\;cm^2.\end{equation}
Por fim, como a área do quadrado vale [tex]100\;cm^2[/tex], a área, [tex]A_5[/tex], do triângulo [tex]\Delta(APN)[/tex] é dada por
\begin{equation}
A_5=100- A_1-A_2-A_3-A_4=100- 2(A_1)-A_4=100-2(25)-20=30\;cm^2.\end{equation}
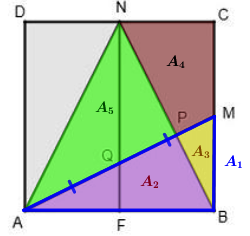
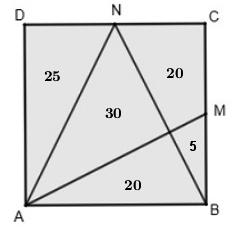
Na figura abaixo, ilustramos a área de cada uma das cinco partes em questão.
Solução elaborada pelos Moderadores do Blog.
