Problema
(Indicado a partir do 9º ano do E. F.)
(Cayley Olympiad, 2013) O desenho mostra um espaço anelar, que é a região entre dois círculos com o mesmo centro. Doze semicírculos iguais tangenciam-se e são colocados dentro do anel. Os diâmetros dos semicírculos estão ao longo dos diâmetros do círculo externo.
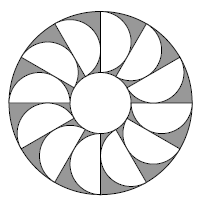
Que fração do anel está sombreada?

Lembretes e notações
✐ Toda tangente a uma circunferência é perpendicular ao raio no ponto de tangência.
✐ A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ.[/tex]
✐ Notações:
– Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X [/tex] e [tex]Y[/tex], por [tex]\angle XVY[/tex] e sua medida por [tex]m\angle{XVY}. [/tex]
– Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Observe que os diâmetros dos doze semicírculos estão igualmente espaçados de [tex]30^\circ[/tex], já que [tex]360^\circ \div 12=30^\circ[/tex].
Considere dois semicírculos adjacentes (veja a figura abaixo). Sejam [tex]A[/tex] o centro do primeiro semicírculo, [tex]B[/tex] o ponto de tangência do primeiro semicírculo com o diâmetro do segundo e [tex]O[/tex] o centro do anel.
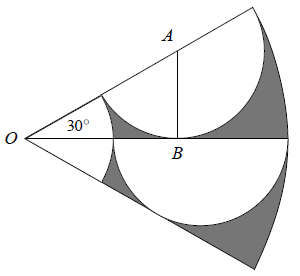
Observe que o ângulo [tex]\angle{ABO}[/tex] é reto, já que, com relação ao primeiro semicírculo, [tex]\overline{OB}[/tex] é uma tangente e [tex]\overline{AB}[/tex] é um raio. Assim, [tex]m\angle{OAB}=60^\circ[/tex], pois as medidas dos ângulos internos do triângulo [tex]OAB[/tex] somam [tex]180^\circ.[/tex]
Sem perda de generalidade, consideremos [tex]AB = 1[/tex]. Desta forma, [tex]OA = 2[/tex], pois quando temos o famoso triângulo de ângulos [tex]30^\circ[/tex], [tex]60^\circ[/tex] e [tex]90^\circ[/tex], sua hipotenusa mede o dobro do cateto oposto ao ângulo de [tex]30^\circ[/tex].
- Concluímos, então, que o raio externo do anel é [tex]3[/tex] e o raio interno é [tex]1[/tex]. Então, a área do anel é dada por [tex]\pi \cdot 3^2 – \pi \cdot 1^2 = \boxed{8 \pi}\,.[/tex]
- Os semicírculos têm raio 1, então doze deles têm área total [tex]12 \cdot \dfrac{1}{2} \cdot \pi \cdot 1^2 = 6 \pi\,.[/tex]
- Assim, a área sombreada é [tex]8 \pi – 6 \pi =\boxed{ 2 \pi}\, .[/tex]
Finalmente, a fração do anel que está sombreada é [tex]\,\fcolorbox{black}{#eee0e5}{$\dfrac{2 \pi}{8 \pi}=\dfrac{1}{4}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
