Problema
(Indicado a partir do 6º ano do E. F.)
(PUC-SP) Um enxadrista quer decorar uma parede retangular de sua casa dividindo-a em quadrados como se fosse um tabuleiro de xadrez.
Sabendo que a parede mede [tex]4,4\;m[/tex] por [tex]2,75\;m[/tex], qual o menor número de quadrados que ele pode colocar na parede?
Solução
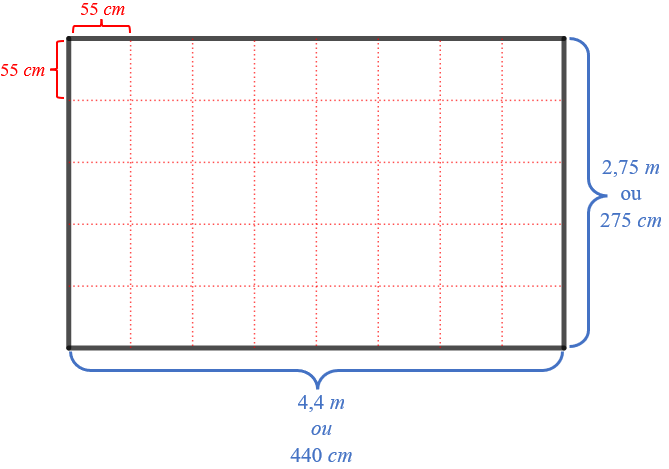
A parede tem largura de [tex]440\, cm[/tex] e altura de [tex]275\, cm[/tex].
Para quadricular essa parede, devemos tomar por base um quadrado cuja medida do lado seja divisor comum de [tex]440[/tex] e [tex]275[/tex]; assim, o menor número de quadrados ocorrerá quando tomarmos o [tex]mdc(440,275) = 55[/tex] como medida do lado do quadrado.
Nesse caso, serão necessários [tex]\dfrac{440}{55}=8[/tex] quadrados na largura da parede e [tex]\dfrac{275}{55}=5[/tex] quadrados na altura, totalizando [tex]8 \times 5 = 40[/tex] quadrados de lados com [tex]55\,cm [/tex] no revestimento da parede.
Solução elaborada pelos Moderadores do Blog .
 |
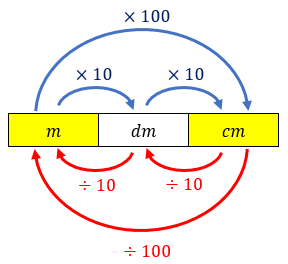
Na conversão de metros (m) para centímetros (cm), o esqueminha abaixo pode ajudar!
|
AJUDA