.Problema: Uma área sombreada II

Problema
(Indicado a partir do 9º ano do E. F.)

A figura abaixo mostra nove quadrados

$1 \text{ cm} \times 1 \text{ cm}$ e um círculo. O círculo passa pelos centros dos quatro quadrados dos cantos.

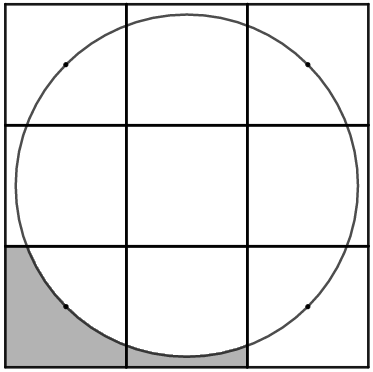
Qual é a área da região sombreada?

Adaptado de Olympiad Cayley – 2011.

Lembretes

(1) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
A área de um círculo de raio $r$ é dada por $A=\pi\cdot r^2$ .

Solução

Considere a região do grande quadrado que fica fora do círculo. Observe, pela simetria da figura, que o centro do círculo coincide com o centro do quadrado do meio e também que a área sombreada da figura inicial (colorida de cinza) ocupa exatamente um quarto da área entre o grande quadrado e o círculo.

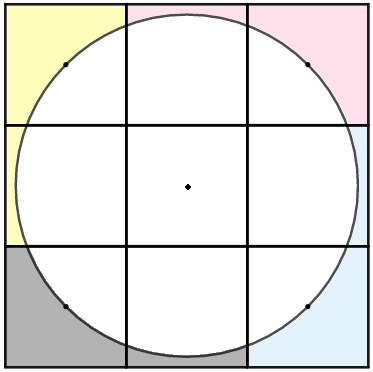
O quadrado externo tem área de $\boxed{9 \text{ cm}^2}$ , sendo composto por nove quadrados $1 \text{ cm} \times 1 \text{ cm}$ .
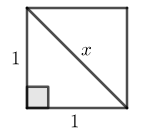
Pelo Teorema de Pitágoras (Lembrete 1), a diagonal de um quadrado $1 \text{ cm} \times 1 \text{ cm}$ tem comprimento $x$ tal que

$\qquad 1^2+1^2=x^2$
$\qquad x^2=2$
e, como $x$ é uma medida,
$\qquad \boxed{x=\sqrt{2}\text{ cm}}$ .

Observamos que o raio do círculo é a distância do centro do quadrado do meio ao centro de um quadrado do canto, então é a soma de duas metades de diagonais, ou seja, tem o comprimento de uma diagonal no total: $r=\sqrt{2}\text{ cm}$ .

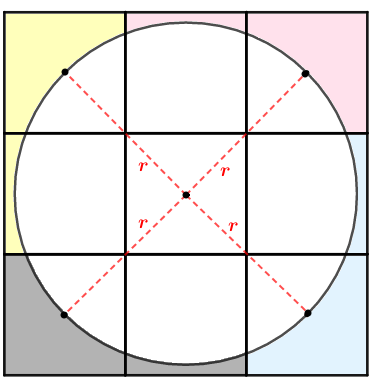
Portanto, pelo Lembrete 2, a área do círculo é:
$\qquad \boxed{\pi\cdot r^2=\pi\cdot(\sqrt{2})^2=2\pi \text{ cm}^2}\,.$

Assim, a área entre o quadrado grande e o círculo é dada por $9-2\pi \text{ cm}^2$ e a região sombreada tem área igual a $\, \fcolorbox{black}{#eee0e5}{$\dfrac{1}{4}\cdot (9-2\pi)=\dfrac{9-2\pi}{4} \text{ cm}^2$}\,.$

Solução elaborada pelos Moderadores do Blog.