Problema
(Indicado a partir do 9º ano do E. F.)
A figura abaixo exibe um semicírculo de raio 10 cm. Os pontos B e C dividem o arco AD em três partes iguais.
Determine a área do “triângulo curvilíneo” ABC.
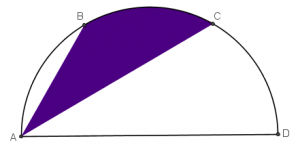
Solução
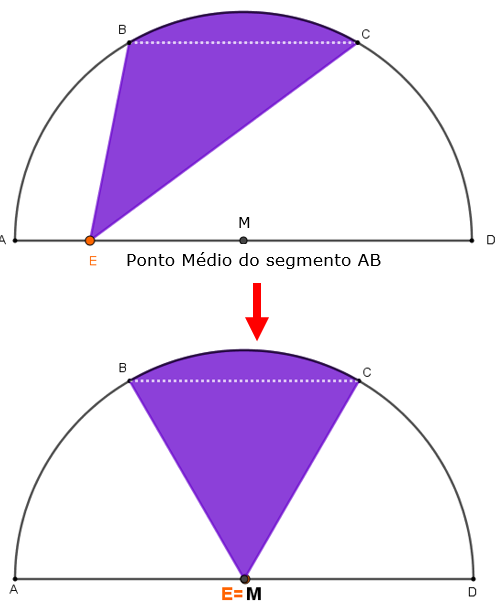
Observe que os segmentos [tex]BC[/tex] e [tex]AD[/tex] são paralelos (procure justificar este fato). Logo, os triângulos [tex]ABC[/tex] e [tex]EBC[/tex] têm mesma área, para qualquer lugar sobre o segmento [tex]AD[/tex] que esteja o ponto [tex]E[/tex]; afinal, teremos dois triângulos de bases iguais (segmento [tex]BC[/tex]) e mesma altura.
Para visualizar esse fato geométrico, utilize o applet abaixo.
Instruções para a utilização:
1) Espere o arquivo carregar completamente.
2) O ponto E pode ser movimentado: é só clicar nele e, mantendo o mouse pressionado, movimentá-lo sobre o segmento AD. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto E e movimente-o.)
OBMEP_srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
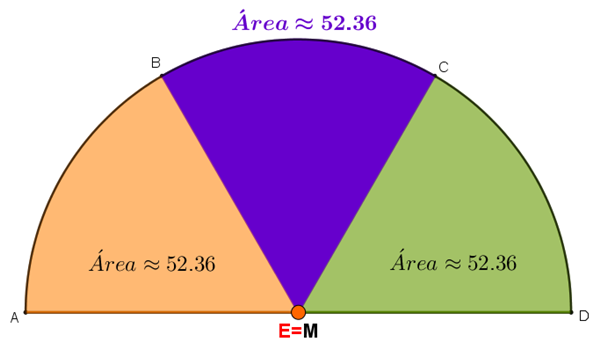
Sendo assim, concluímos que a área da figura pintada de roxo, triângulo curvilíneo [tex]ABC[/tex], corresponde a um terço da área do semicírculo.
Para convencer-se disto, movimente o ponto [tex]E[/tex] no próximo applet, colocando-o sobre o ponto médio do segmento [tex]AD[/tex], conforme mostra a figura a seguir, e observe que, neste caso, o semicírculo fica dividido em três regiões iguais.
Instruções para a utilização:
1) Espere o arquivo carregar completamente.
2) O ponto E pode ser movimentado: é só clicar nele e, mantendo o mouse pressionado, movimentá-lo sobre o segmento AD. (Se você estiver utilizando um celular ou um tablet, toque levemente no ponto E e movimente-o.)
OBMEP_srdg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
Dessa forma, a área do triângulo curvilíneo [tex]ABC[/tex] é dada por:
[tex]\qquad \qquad Área= \dfrac{\, \dfrac{\pi r^2}{2}\, }{3}=\dfrac{\pi 10^2}{6}=\dfrac{50\pi}{3}\ \approx ~ 52,36~cm^2[/tex].
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube: Mini-einstein’s.
